9.Прочность при переменных напряжениях.
Характеристика цикла напряжений:
Максимальное напряжение( наибольшее по модулю) δmax или τmax;
Минимальное напряжение (наименьшее по модулю) δmin или τmin;
Среднее напряжение
где
-
максимальное напряжение( по модулю);
-
минимальное напряжение (по модулю);
амплитуда напряжений
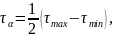
коэффициент асимметрии
Значение
,
,
могут быть положительными, отрицательными
и равным нулю. Амплитуда всегда
положительна.
При напряжениях, переменных во времени, расчёты на прочность на практике обычно бывают проверочными.
нормативный
коэффициент запаса прочности данной
детали при данном цикле напряжений.
Коэффициент запаса прочности при симметричном цикле равен отношению предела выносливости материала детали к максимальному напряжению цикла:
при изгибе :
при кручении:
где
-
масштабные коэффициенты при изгибе и
кручении;
,
-
пределы выносливости при симметричном
цикле.
При несимметричных циклах и любом виде деформации
где
,
-
коэффициенты, учитывающие чувствительность
материала к асимметрии цикла при
соответствующем нагружении (приводятся
в справочниках в зависимости от предела
прочности материала);
-
коэффициент качества поверхности;
эффективный коэффициент напряжений
где
-предел
выносливости с симметричным циклом
изменения напряжений при наличии
концентратов напряжений.
Влияние
качества обработки поверхности детали
на предел выносливости материала
учитывающий коэффициент качества
поверхности
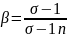
где
-
предел выносливости образца полированной
поверхностью.
При сложном напряжённом состоянии коэффициент запаса прочности детали вычисляют так:
Кроме коэффициента запаса прочности детали по сопротивлению материала усталости необходимо вычислить коэффициент запаса прочности по сопротивлению его пластическим деформациям:
Расчётным
является меньший из коэффициентов
запаса прочности s
и
Амплитуда напряжений
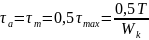
где
-
момент сопротивления кручению.
10.Зависимость между моментами инерции относительных параллельных осей. Понятие о главных осях и о главных моментах инерции.
Осевые моменты инерции- взятая по всей площади сечения сумма произведений площадей элементарных площадок на квадраты расстояний от них до этой оси. Рис 1
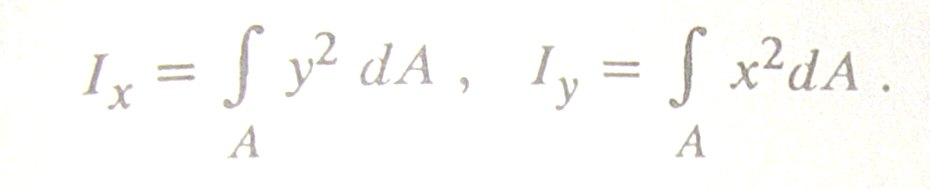
Рис1
Полярный момент инерции сечения определяют по формуле рис 2
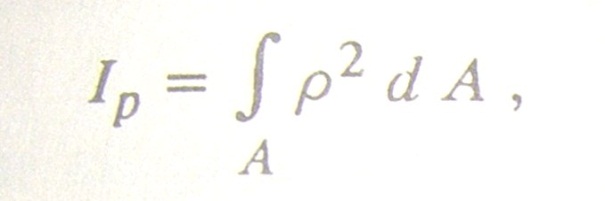
Рис2
Где р- расстояние от площадки dA до точки, относительно которой вычисляется полярный момент инерции, Следовательно(Рис 3)
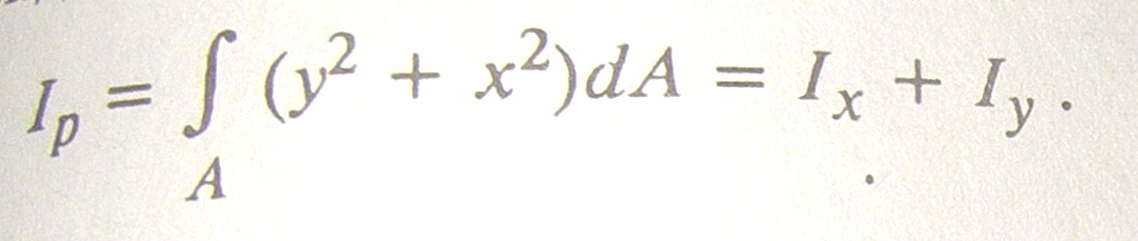
Рис3
Моменты инерции, содер. Под интегралом координаты во второй степени, всегда положительные. Центробежный момент инерции содержит произведение координат в перв степени и в зависимости от положения осей может быть положительным, отрицательным или равным нулю.
Значения моментов инерции зависят от положения осей координат .Можно установить след зависимость между моментами инерции при параллельном переносе осей координат(рис 4)
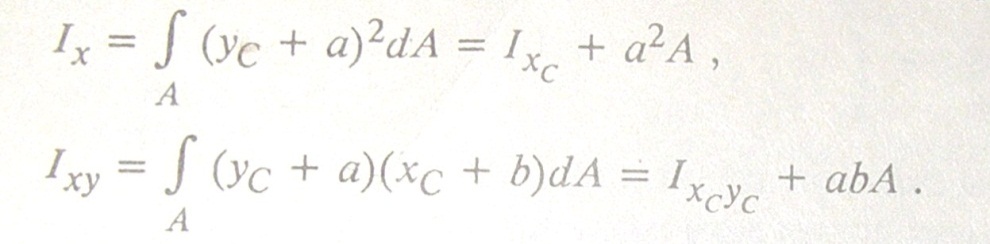
Рис4
Ось Cx Cy являются центральными.
Главные оси и главные моменты инерции. При повороте осей координат на некоторый угол a относительно точки О( рис 5) значения осевых моментов инерции изменяются, но их сумма остаётся постоянной: Ix1+Iy1=Ix+Iy=const.
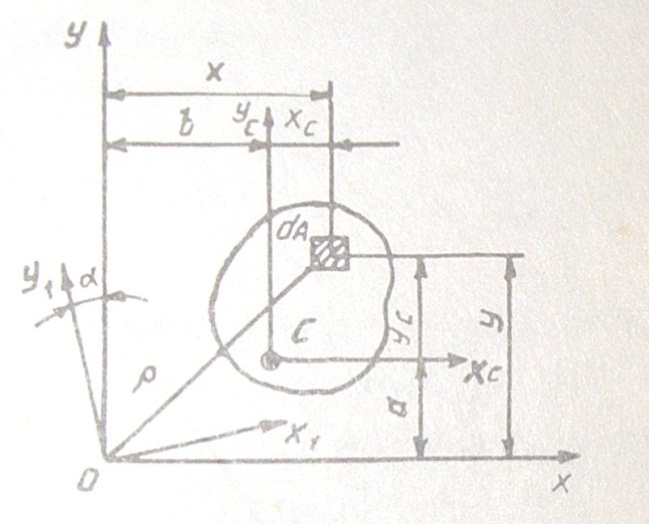
Рис 5
Главными осями инерции сечения –наз. Оси, относительно которых центробежный момент инерции сечения равен нулю, а осевые моменты инерции экстремальные значения.Главные оси, проходящие через центр тяжести сечения, наз. его главными центральными осями.
Для симметричных сечений оси их симметрии являются главными осями инерции.
Положение главных осей инерции относительно других осей определяют, используя соотношение (рис6)
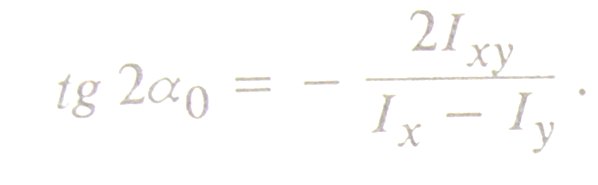
Рис6
Осевые моменты инерции относительно главных осей называются главными моментами инерции.(рис 7)
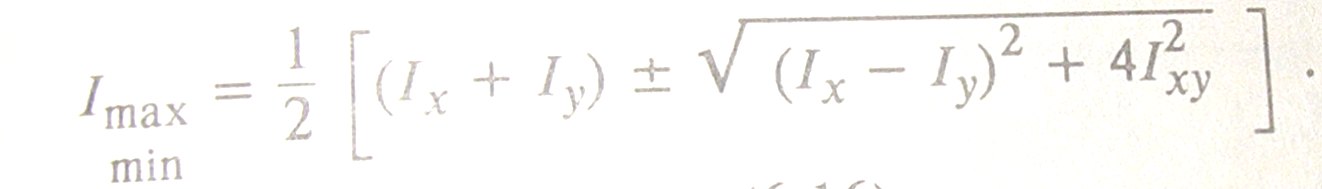
Рис7