1 Растяжение-сжатие. Напряжения и перемещения. Условия прочности.
Растяжение-сжатие —вид продольной деформации стержня или бруса (брус-ЭК, работающий на растяжение, сжатие), возникающий в том случае, если нагрузка к нему прикладывается по его продольной оси.
Называется также одноосным или линейным напряжённым состоянием. Вызывается как силами, приложенными к концам стержня, так и силами, распределёнными по объёму (силы инерции и тяготения).
Растяжение вызывает удлинение стержня (также возможен разрыв и остаточная деформация), сжатие вызывает укорочение стержня (возможна потеря устойчивости и возникновение продольного изгиба). Растягивающие продольные силы принято считать положительными, а сжимающие-отрицательными.
В поперечных сечениях бруса возникает— нормальная сила. Если растягивающая или сжимающая сила параллельна продольной оси бруса, но не проходит через неё, то стержень испытывает сжатие. В этом случае возникают ещё и изгибные напряжения.
При
упругой
деформации
(деформация,
исчезающая после прекращения действий
внешних сил и тело принимает первоначальные
размеры и форму) между напряжением и
относительной деформацией определяется
законом
Гука
.
(где Е – коэф. Пропорциональности, модуль
продольной упругости)
При растяжении и сжатии бруса меняются его продольные и поперечные размеры.
При
растяжении:
Длина бруса меняется на
(удлинение),
Ширина бруса меняется на
(сужение).
При
сжатии:
(укорочение)
(увеличение
Закон Гука
выражает прямо
пропорциональную зависимость между
нормальным напряжением и относительной
деформацией:
Деформация бруса (растяжение или сжатие) вызывает перемещение поперечных сечений.
При
центральном растяжении (сжатии) в
поперечном сечении возникают нормальные
напряжения:
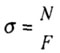где N - продольная сила; F - площадь
поперечного сечения. Эти напряжения
распределены по поперечному сечению
равномерно
Напряжения
Сосредоточенные внутренние силы и их моменты, характерезующие взаимодействие отдельных частей тела, являются лишь статистическим эквивалентом внутренних сил ,распределенных по площади сечения. Мерой их интенсивности является напряжение, представляющее предел отношения элементарного усилия, действующего на элементарной площадке, к ее площади:
р= lim ∆R/∆A
(в качестве ед. измерения считают 1 Па=1Н/м^2)
Если силу ∆R разложить на 2 составляющие- нормальную ∆N и косательную ∆Q , действующую в плоскости сечения, то по ним можно определить нормальное ơ и касательное ῐ напряжения.
Ơ= lim ∆N/∆A (∆A-> 0), ῐ = lim ∆Q/∆A (∆A-> 0)
Перемещения
Под действие внешних сил тело дефрмируется. Первоначальное положение его сечений меняется.Перемещение сечений вдоль линии называется линейным, а перемещения, ввязывающие поворот линий и плоскостей-угловыми.
Условие прочности (задача) – определить оценку прочности конструкции, через сравнение расчетных напряжений с допускаемыми:
- расчетное
касательное напряжение.
Условие прочности бруса при его растяжении (сжатии):
Ơ=N/A<= [Ơ]
Пример: проверить прочность бруса,если матириал Ст3, [Ơ]=160МПа, а площадь поперечного сечения А=200 мм^2.
Решение: Ơmax =Nmax/A=(30*10^3)/200=150МПа< [Ơ]