26. Моделі, які зводяться до моделі простої (множинної мне кажется тут опечатка) лінійної регресії. Приклади застосування простої лінійної регресії.
Багато економічних процесів найкраще описувати нелінійними співвідношеннями. Проте дуже часто існує можливість за допомогою різноманітних математичних операцій звести такі функції до лінійних, які елементарно оцінити за допомогою моделі простої лінійної регресії.
Нехай, досліджувана модель має такий вигляд:
.
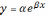Щоб привести цю модель до простої лінійної регресії, слід зробити такі зміни:
Логарифмувати обидві частини рівняння:
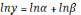
Позначити отримані величини:
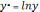
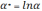
Записати рівняння простої лінійної регресії:
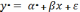
Основні види перетворень для зведення моделей до простої лінійної регресії наведено в таблиці.
-
№
Початкова функція
До якого виду приводимо
Заміна змінної
1
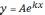
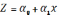
Z=lny,
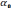=lnA,
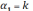
2
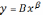
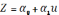
Z=lny, u=lnx, =lnB,
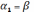
3
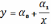
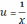
4
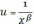
Слід зазначити, що не всі моделі можна звести до простої лінійної регресії, наприклад:
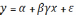
У цій
моделі неможливо однозначно визначити
окремо коефіцієнти
,
тому цю модель неможна звести до простої
лінійної регресії.
27. Множинна лінійна регресія. Структура моделі та основні припущення при її побудові. Оцінка моделі.
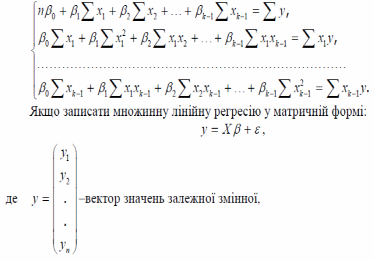
28. Моделі, які зводяться до моделі множинної лінійної регресії.
За допомогою стандартних математичних перетворень можна велику кількість моделей звести до множинної лінійної регресії. Наприклад, розглянемо виробничу функцію Кобба-Дугласа
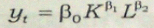
Де
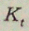– основні фонди підприємства;
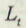– обсяг фонду оплати праці;
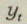– випуск продукції.
Прологарифмувавши рівняння, маємо:
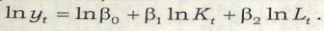
Введемо нові позначення:
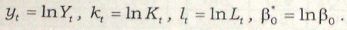
Тоді модель можна записати у вигляді
Якщо ввести до цього рівняння стохастичний доданок, то одержимо модель лінійної регресії
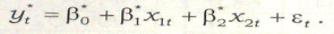
Аналогічно модна вивчати досить широкий клас моделей, які за допомогою перетворень змінних і рівнянь можливо звести до моделі лінійної регресії. Досить часто використовують поліноміальну регресію.
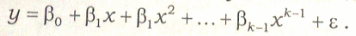
Проте в разі використання поліноміальної регресії спостерігається явище мультиколінеарності.
29. Виділення сезонних коливань
Ряд значень, взятих за певний часовий період, називається часовим рядом. Для того, щоб оцінити поведінку таких рядів, доцільно розділити ці значення на декілька складових. Ці складові можна розглядати як: тренд, циклічні, сезонні та випадкові коливання. Сезонні коливання — демонструють періодичність коливань протягом року (наприклад, обсяг продажу в зимові місяці вищий, в літні місяці він знижується, а восени знову починає зростати). Сезонні коливання можна вичленувати після аналізу тренду і циклічних коливань. Сезонна складова може бути очевидна в багатьох випадках, де задіяні фінансові й економічні показники. При оцінці сезонних коливань найчастіше використовуються два методи: Метод складування використовується у випадках, коли сезонні складові відносно постійні по всьому часовому періоді, що аналізується. При цьому значення часового ряду можна подати як суму тренду сезонної складової: Xі = Ті+ Sі , де: Xі — фактичне значення в періоді і; Ті — тренд у періоді і; Sі — сезонне відхилення в періоді і. Розділ 6 Метод множення використовується, коли сезонні складові змінюються пропорційно значенням тренду по всьому часово-му періоду, що аналізується. У цьому випадку значення Т часового ряду можна подати як добуток тренду і сезонної складової. При цьому формула має такий вигляд: Xі = Ті* Sі .
Для визнач сезонних коливань будуємо модель виду:
де 1 q – фіктивна змінна, що приймає значення 1, якщо розглядається перший квартал року, 0 – в інших випадках,
2 q – фіктивна змінна, що приймає значення 1, якщо розглядається другий квартал року, 0 – в інших випадках,
3 q – фіктивна змінна, що приймає значення 1, якщо розглядається третій квартал року, 0 – в інших випадках,
t – трендовий компонент, що показує зростання прибутків протягом часу спостережень.