58. Стаціонарність часових рядів

Якщо часовий ряд стаціонарний, що означає наявність статистичної рівноваги щодо постійної середньої с, він може бути представлений широким класом лінійних моделей, що називаються моделями авторегресії-ковзного середнього.

Часовий ряд (процес) називається стаціонарним якщо:

1. математичне сподівання скінченне й постійне: Мy_t=μ<∞ для всіх t=0,± 1,± 2,…;

2. дисперсія скінченна й постійна: Dу_t =γ₀ <∞ для всіх t=0,± 1,± 2,…;

3. значення автоковаріаційної функції залежать лише від різниці аргументів: автоковаріація j-го порядку cov(у_t, у_t-j) = γ_j < ∞ для всіх t=0,± 1,± 2,…, j = 1,2,3,…

Важливою характеристикою стаціонарних випадкових процесів є автокореляційна функція. Автокореляцію j-го порядку визначають за допомогою рівності

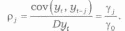
Зауважимо, що р₀ =1, р_j = р_-j. Отже, достатньо розглядати послі­довність p_J лише для натуральних j. Ця послідовність називається автокореляційною функцією.

У теорії випадкових процесів розрізняють два поняття стаціонарності: стаціонар­ність у вузькому та широкому розумінні. Ми розглядаємо лише стаціонарність у широкому розумінні.

59. Метод усереднення

Одним із методів згладжування часового ряду є метод рухомого середнього (усереднення). Суть полягає у заміні початкового часового ряду послідовністю середніх, що обчислюються на відрізку, який переміщується вздовж часового ряду. Задається довжина відрізка ковзання (2m+1) по часовій осі, тобто береться непарна кількість спостережень. Підбирається поліном: 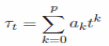до групи перших (2m+1) членів ряду, і цей поліном використовується для визначення значення тренду у середній (m+1)-й точці групи. Потім провадиться зсув на один рівень ряду вперед і підбирається поліном того ж порядку до групи точок, що складається з 2-го, 3-го,. . . , (2 m +2)-го спостереження. Знаходиться значення тренда в (m +2)-й точці і т.д. тим же способом уздовж всього ряду до останньої групи з (2m +1) спостереження. Насправді немає необхідності будувати поліном для кожного відрізка. Як буде показано, ця процедура еквівалентна знаходженню лінійної комбінації рівнів часового ряду з коефіцієнтами, які можуть бути визначені раз і назавжди і залежать тільки від довжини відрізка ковзання і ступеня полінома.

Для визначення коефіцієнтів a0, a1,. . . , а_р полінома за допомогою методу найменших квадратів за першим (2 m + 1) точкам мінімізується функціонал:

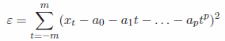
Зауважимо, що t приймає умовні значення від-m до m. Це досить зручний прийом, істотно спрощує розрахунки. Диференціювання функціоналу по a0, a1,. . . , а_р дає систему з р + 1 рівняння типу:

Рішення цієї системи рівнянь щодо невідомих параметрів a0, a1,. . . , а_р полегшується тим, що 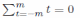і всі суми від t-m до m непарних порядків 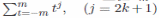теж рівні нулю. Крім того, т.я. поліном, підібраний за 2m +1 точками, використовується для визначення значення тренда в середній точці, а в цій точці t = 0, то, поклавши в рівняння t = 0, отримуємо значення тренда, рівне а₀. Стало бути, завдання зводиться до пошуку а₀.

Система нормальних рівнянь, яку потрібно вирішити відносно а₀, розбивається на дві підсистеми: одна - містить коефіцієнти з парними індексами а0, а2, а4,. . . , Інша - включає коефіцієнти з непарними індексами а1, а3, а5,. . . . Рішення системи щодо a₀ залежить від чисельних значень 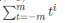лінійних функцій від х типу

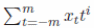
У підсумку, значенням тренда в центральній точці відрізка буде середня арифметична, зважена із значень часового ряду від х_-м до х_м з ваговими коефіцієнтами βt, які залежать від значень м і р:

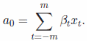
Зазначена процедура повторюється для всіх наступних відрізків ковзання, з обчисленням значень тренду в їх середніх точках.