42. Методи визначення автокореляції

Оскільки автокореляція є негативним явищем, потрібно вміти його тестувати. Найбільш відомим і поширеним тестом перевірки моделі на наявність автокореляції залишків є тест Дарбіна-Уотсона. Цей тест використовується для авторегресійних схем 1-го порядку і має наступний алгоритм Алгоритм тесту Дарбіна - Уотсона

Крок 1. Виходячи з відсутності автокореляції залишків на основі методу найменших квадратів будується економетрична модель і обчислюються її залишки .

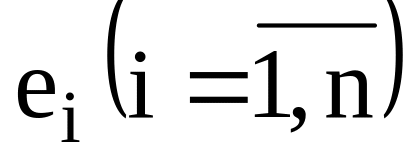Крок 2. Розраховується статистика (критерій) Дарбіна-Уотсона за наступною залежністю :

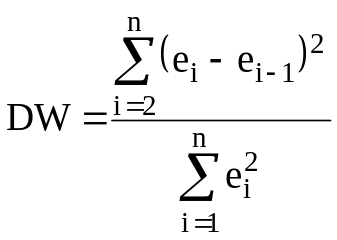(7.8)

Крок 3. Задаючись рівнем значимості , для числа факторів моделі m і числа спостережень n за статистичними таблицями DW - розподілу Дарбіна-Уотсона, визначаються два значення d_L , і d_U.

Крок 4. Будуються зони автокореляційного зв’язку, які схематично можна представити в наступному вигляді:

Рис. 7.2 - Зони автокореляційного зв’язку

Крок 5. На основі розрахункового значення критерію DW роблять висновок щодо наявності або відсутності автокореляції залишків :

• якщо - це свідчить про наявність позитивної автокореляції залишків ;

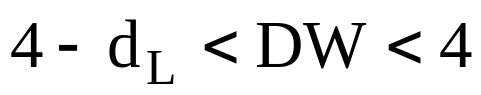• якщо - це свідчить про наявність негативної автокореляції залишків;

• якщо 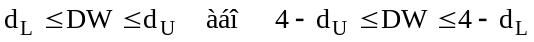- неможливо зробити висновок ні про наявність, ні про відсутність автокореляції залишків ;

• якщо 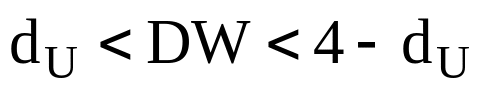- автокореляція залишків відсутня .

Узагальнений метод найменших квадратів.

Будемо вважати, що для регресії

y =Xβ+v (1)

кореляційна матриця Σ відома.

Введемо наступні позначення:

Σstepen'(- ½) y = y* ,

Σstepen'(- ½)X=X*,

Σstepen'(- ½) v= ε.

З урахуванням уведених позначень маємо:

y*=X*β + ε (2).

Оцінкою узагальненого МНК коефіцієнтів моделі (1) називається оцінка

звичайного МНК, знайдена за моделлю (2).

Процес авторегресії першого порядку AR(1).

v i = ρvi-1+ εi ,i= 1,n.

У випадку AR(1)–збурень кореляційна матриця Σ записується у вигляді

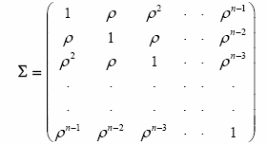
Це дає можливість знайти змінні для узагальненого методу найменших

квадратів у явному вигляді:

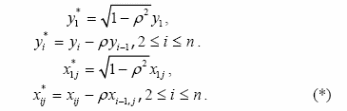
Якщо у вихідній моделі є постійний доданок, то перетворена модель не

матиме константи. Замість неї з’явиться змінна x* 0

, значення якої дорівнюють

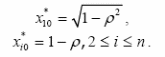
Оцінка параметра ρ .

Вибірковий коефіцієнт кореляції залишків методу найменших квадратів

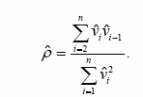
Оцінка Дарбіна-Уотсона.

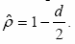
Метод Дарбіна.

Формула (*) записується у вигляді

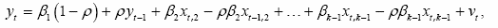
тобто y t −1 включається в число регресорів, а ρ – в число параметрів, що

оцінюються. Для цієї регресії за допомогою звичайного МНК знаходяться

оцінки ˆ ρ та ˆ θj параметрів ρ та ρβj відповідно. В якості оцінки ˆ

βj беруть ˆ θj / ˆ ρ.

Можна покращити якість оцінок ˆ βj , підставивши отримане значення ˆ ρ до (*), і знайти нові МНК-оцінки параметрів ˆ βj.

Метод Кочрейна-Оркатта.

Ітеративно обраховуються формули (*),

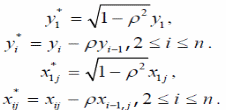залишки за узагальненим методом

найменших квадратів, поки не буде досягнуто необхідної точності.

Метод Хілдрета-Лу.

Обчислюється модель при всіх ρ з інтервалу від -1 до 1 з кроком 0.01.

Вибирається те значення, при якому сума квадратів відхилень в узагальненому

Методі найменших квадратів мінімальна.