2. Прогнозирование параметра состояния конкретного элемента по его реализации.

При прогнозировании по реализации изменение параметра состояния элемента (изделия, машины) определяется экстраполяционной функцией и среднеквадратическим отклонением этой функции от фактического изменения параметра состояния. Для каждого элемента изменению параметра состояния соответствует определенное допустимое (в частности, предельное) значение параметра. Преимущество метода прогноза по реализации заключается в значительном уменьшении вариации изменения параметра элемента, так как математичесмкое ожидание случайной величины заменяется ее реализацией. Однако получение сведений о наработке каждого элемента и допустимых значений параметра состояния связано с большими трудностями.

В качестве целевой функции при прогнозировании принимается степенная функция (этапом приработки – пренебрегаем)

u(t) = v_c t^ + z , (24)

В данной ситуации v_c – это фиксированное число, определяемое (как и показатель степени) по эксплуатационным данным, а z – случайная величина, характеризующая отклонение реальных данных от усредненной кривой. На нее оказывают влияние как случайные эксплуатационные режимы, так и погрешность определения значения v_c для элемента. Считается, что распределение случайной величины z подчиняется нормальному распределению (в сечении t = T_P (см. формулу (18)), соответствующем предельному значению параметра состояния, u_P), причем дисперсия этого распределения _Z находится из имеющихся данных о наработке ( от 0 до t). Таким образом, можно определить плотность распределения z в виде:

f(u – u_P) = . (25)

Плотность распределения (25), и соответствующая функция распределения Лапласа позволяют оценивать вероятность отказа элемента для различных времен наработки и соответствующих значений параметра состояния, и тем самым, решать различные задачи.

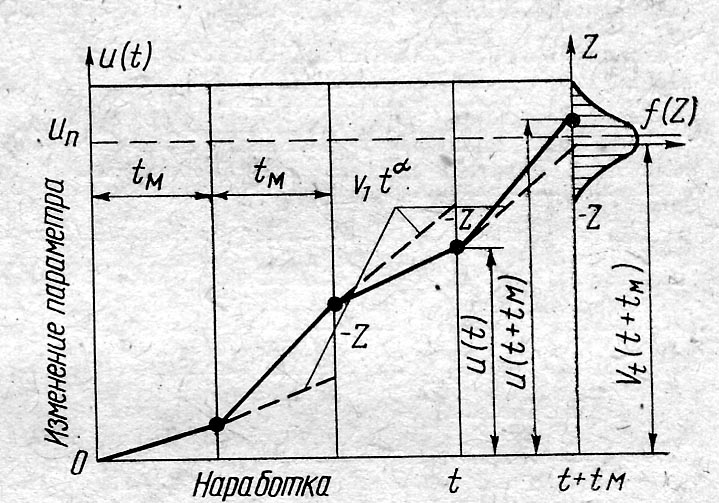
При прогнозировании по реализации принимают, что в текущий момент t была проведена диагностика машины, и определено изменение параметра u(t) . Метод прогнозирования позволяет решить следующие задачи:

1. Если задана межремонтная (межконтрольная) наработка t_M , то необходимо определить, не превышает ли экстраполируемое значение u(t+t_M) допустимого значения параметра u_D (в частности, предельного), если машина должна еще работать межремонтный период t_M

2. Если межремонтная наработка t_M не задана, то требуется найти остаточный ресурс машины (элемента), который соответствует достижению предельного значения параметра состояния машины (элемента).

Для решения обеих задач надо определить остаточный ресурс t_AD

по времени, и сравнить ее с межремонтным периодом. Таким образом, из соотношения

u(t + t_AD) = v_C (t + t_AD)^ =u(t) (1 + t_AD / t )^ = u_P . (26)

определяем остаточный ресурс по формуле

t_AD = t [ (u_P / u(t))^ - 1 ]. (27)

Сравнивая величину t_AD с t_M , получим ответ на поставленные задачи.

3. Плотность функции распределения (25) определяет рассеивание отклонения для данного конкретного элемента. С ее помощью можно оценить вероятность отказа элемента, который наступает при превышении значения u параметра состояния предельного значения u_P , то-есть величину Q(t_M ) = Q[u(t + t_M) > u_P ], то-есть вероятность того, что значение u(t + t_M) окажется больше, чем u_P. Для этого следует по (25) вычислить соответствующую вероятность:

Q(t_M ) = Q[u(t + t_M) > u_P ] =  [(u(t + t_M ) - u_P) / _Z ] . (28)

Здесь  [(u(t + t_M ) - u_P) / _Z ] – интегральная функция нормированного нормального распределения Лапласа (из таблицы 3 – см. ниже).

При этом вероятность отказа Q(t_M ) определяется величиной безразмерного аргумента

Z = (u(t + t_M ) - u_P) / _Z .

В таблице 3 приведены значения нормированной функции Лапласа (вероятности отказа) в зависимости от безразмерного аргумента.

Таблица 3.

Z	-2	-1	-0.5	0	0.5	1	2
Q(tM )=(Z)	0.03	0.16	0.307	0.5	0.693	0.84	0.97