
- •1.Классификация электроакустической аппаратуры
- •2. Основные принципы преобразования энергии, используемые при конструировании эап
- •Преобразователи с магнитным полем
- •Электродинамический преобразователь
- •2. Электромагнитный преобразователь
- •Преобразователи с электрическим полем
- •1. Электростатический преобразователь
- •2.Пьезоэлектрический преобразователь
- •3.Направленность излучателей звука
- •4.Направленные свойства приёмников звука.
- •5. Числовые методы описания хн преобразователей Числовые характеристики хн
- •6.Коэффициент осевой концентрации как числовая характеристика направленности преобразователей.
- •7. Характеристика направленности двух синфазных точечных источников.
- •8. Характеристика направленности линейной эквидистантной группы точечных преобразователей
- •9. Характеристика направленности линейного сплошного излучателя.
- •10. Характеристика направленості круглогопульсуючого поршня
- •11. Метод электромеханических и электроакустических аналогий
- •12. Сопротивление излучения круглого поршня при работе в бесконечном экране (пульсирующий поршень)
- •13. Сравнение эффективности излучения круглого поршня в экране и без внешнего оформления
- •14. Сопротивление излучения и оценка эффективности излучения полупоршнем
- •15. Классификация и основные технические характеристики громкоговорителей
- •16. Устройство диффузорного электродинамического громкоговорителя.
- •17. Элементы конструкции электродинамического громкоговорителя и материалы, применяемые для их изготовления.
- •18. Согласование характеристик электродинамического громкоговорителя.
- •19. Механическая чувствительность громкоговорителя и требования к выбору параметров механической системы.
- •20. Схема электрического аналога громкоговорителя.
- •21. Вносимое сопротивление громкоговорителя.
- •22.Частотная характеристика входного сопротивления громкоговорителя
- •23. Нелинейные искажения громкоговорителя
- •24.Параметрические и модуляционніе искажения
- •25.Внешнее оформление громкоговорителя в виде щита
- •26.Внешнее оформление громкоговорителя в виде открытого ящика
- •27.Внешнее оформление громкоговорителя в виде закрытого ящика
- •28. Внешнее оформление громкоговорителя в виде фазоинвертора.
- •29. Волновое уравнение в бесконечном рупоре
- •30. Решение уравнения Вебстера для бесконечного экспоненциального рупора.
- •31. Анализ звукового поля в бесконечном экспоненциальном рупоре.
12. Сопротивление излучения круглого поршня при работе в бесконечном экране (пульсирующий поршень)
При любом движении тела в среде, это тело встречает со стороны среды сопротивление – силу противодействия среды.
В задаче излучения звука это сопротивление носит название сопротивления излучения. По сути, - это нагрузочное сопротивление со стороны, или сопротивление, на котором "выделяется"излучаемаяакустическая мощность.
По определению, сопротивлением излучения называется отношение силы реакции среды к колебательной скорости тела:
 ,
,
где 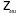 –
механическое сопротивление излучения,
–
механическое сопротивление излучения,
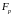 –
сила реакции среды,
–
сила реакции среды,
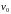 –
колебательная скорость излучателя.
–
колебательная скорость излучателя.
В общем случае, – комплексная величина, размерная:
 ,
,
где
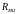 и
и
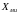 – соответственно, активная и реактивная
составляющие сопротивления излучения.
– соответственно, активная и реактивная
составляющие сопротивления излучения.
Величина определяется однозначно, когда поверхность излучения характеризуется одинаковой скоростью движения .
Для определения необходимо представить поверхность излучателя S в виде совокупности элементарных излучателей площадью dS, определить на каждом излучателе создаваемое соседними излучателями давление PS и произвести интегрирование вида:
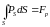 .
.
Эквивалентная схема излучателя представляется в виде:
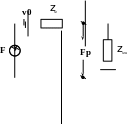
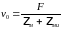
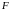 –внешняя сила,
–внешняя сила,
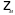 –механическое сопротивление
излучателя.
–механическое сопротивление
излучателя.
Особенностью излучения в
воздухе является условие
 ,
что обусловливает низкий К.П.Д. ЭАпп
(
,
что обусловливает низкий К.П.Д. ЭАпп
(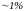 ).
Тогда
).
Тогда
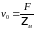 .
.
Сопротивление излучения круглого поршня при работе в бесконечном экране (пульсирующий поршень)
Активная
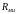 и реактивная
и реактивная
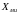 составляющие сопротивления излучения
имеют следующую конструкцию:
составляющие сопротивления излучения
имеют следующую конструкцию:
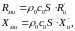
тогда
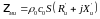
где 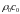 –
волновое сопротивление среды,
–
волновое сопротивление среды,
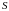 –
площадь излучателя;
–
площадь излучателя;
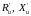 –
безразмерные множители, зависящие от
конструкции излучателя.
–
безразмерные множители, зависящие от
конструкции излучателя.
При помещении поршня в
полубесконечную трубу поршень излучает
плоскую волну
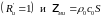 :
:
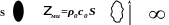
Таким образом, максимальное
значение
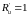 .
.
В случае круглого поршня в
бесконечном экране аналитические
выражения
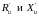 :
:
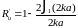
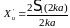
где
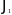 –функция
Бесселя 1-го порядка,
–функция
Бесселя 1-го порядка,
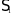 – функция Струве 1-го порядка,
– функция Струве 1-го порядка,
а – радиус поршня.
Асимптотические выражения выглядят следующим образом:
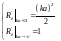 ;
;
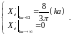
Г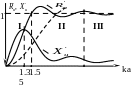 рафики
функций
рафики
функций
 :
:
Пунктиром нанесен график
для
 сферическогоизлучателя.
сферическогоизлучателя.
В области малых kа (область I) преобладает
реактивная составляющая
 .
.
В области больших kа
(область II) преобладает активная составляющая . Причем, в случае поршня имеем существенный выигрыш в излучаемой мощности по сравнению со сферическим излучателем:
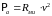 .
.
В области III при kа → ∞ составляющей вообще можно пренебречь.
Определим характер реактивности сопротивления.
Для этого рассмотрим низкочастотную асимптотику :
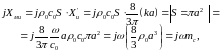
где mс–соколеблющаяся масса среды,
 .
.
Итак, реактивность поршня носит инерционный характер. В электромеханической аналогии:
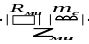
Все приведенные выражения дают количественную оценку механического сопротивления излучения при расчете его для одной стороны излучателя. Для определения характеристик с обеих сторон необходимо все полученные выражения умножить на 2.
