8. Характеристика направленности линейной эквидистантной группы точечных преобразователей

Рассматриваем группу N ненаправленных преобразователей равной производительности, располагающихся на одной прямой с постоянным шагом d (линейная эквидистантная группа).

pис.6.1

Полярная ось проходит через центр базы (направление максимального излучения).

Выберем удаленную т. на расстоянии 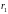от первого источника и под углом 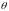. Лучи, идущие от всех источников в т.А, считаем параллельными.

Обозначим через 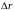разность хода звуковых лучей от первого и второго источника:

, .

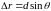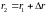Потенциал скоростей первого источника в т.А: .

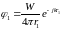Потенциал второго источника

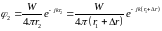
, поэтому пренебрегаем в амплитудной части:

.

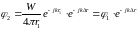Разность хода звуковых лучей от третьего и второго источника также составляет , следовательно

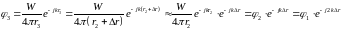
По аналогии запишем потенциал скоростей N-ого источника: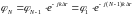

Для нахождения ХН следует найти 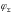и пронормировать на его максимальное значение. Результирующий потенциал:

Слагаемые образуют геометрическую прогрессию. Можно воспользоваться готовой формулой для суммы членов.

Для понимания физической сущности процесса предлагается сложить векторы геометрически.

Векторы равны по модулю (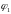 ) и сдвинуты друг относительно друга на один и тот же угол 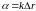. Следовательно, все векторы будут представлять собой хорды окружности. При этом, система наиболее эффективна, если совпадает с диаметром окружности. В случае, когда крайние излучатели находятся в противофазе (сдвиг на полдлины волны), они гасят друг друга и суммарная эффективность системы падает.

Проведем окружность произвольного радиуса. Отложим отрезок, пропорциональный . Вектор 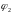отложим под углом к и т.д.

pис.6.2

Рассмотрим 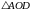(рис.6.2):

; , , .

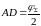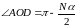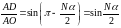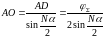Из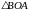 : 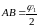; 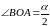, , 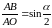,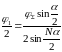откуда

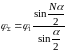
Найдем максимальное значение при функции , учитывая, что .

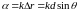Заменим синус малого угла аргументом:

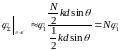
Следовательно, .

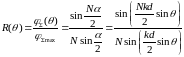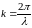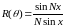Учитывая, что , представим выражение для ХН в виде: , где .

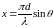9. Характеристика направленности линейного сплошного излучателя.

Рассмотрим бесконечно тонкий пульсирующий цилиндр длиной 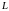(в поперечном сечении - точечный излучатель).

рис. 7.1

Представим такой цилиндр линейной группой N точечных излучателей, расстояние между которыми 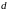. Тогда длина цилиндра

.

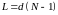Устремим 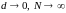. Приблизительно можно считать: .

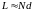Выражение для ХН пульсирующего цилиндра получим из выражения для ХН линейной группы N точечных излучателей при (заменяя ):

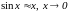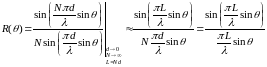
Запишем выражение для ХН в ви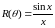де , где .

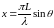График функции :

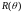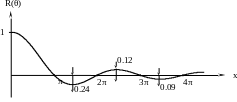
рис.7.2

Функция убывающая, следовательно ХН будет содержать только один главный лепесток, а остальные – дополнительные (убывающие).

Пусть , ; , .

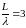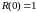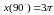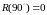рис.7.3

10. Характеристика направленості круглогопульсуючого поршня

Представимо|уявимо| випромінюючу поверхню поршня набором точкових випромінювачів. Знайдемо їх сумарний потенціал в дальньому|далекому| полі і пронормуємо на максимальне значення.

Поршень радіусу а; –коливальна швидкість на поверхні поршня.

Розмістимо поршень в площині|плоскості| . Виберемо т. на відстані від центру поршня під кутом|рогом,кутком| до осі (у площині|плоскості| ). Виділимо елементарне джерело на поверхні поршня на відстані від центру під кутом|рогом,кутком| . Площа|майдан| елементарного джерела

.

Відстань від елементарного джерела до т. А позначимо h, тоді елементарний потенціал в т. А:

,(беремо половину тілесного кута|рогу,кутка| ( ), оскільки випромінювання в напівпростір).

Рис. 3.49

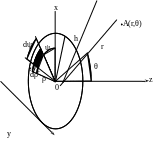
Повний|цілковитий| потенціал всіх елементарних джерел в т. А:

.

Необхідно визначити h.

Координати точкового джерела:

Координати в т. А:

Тоді

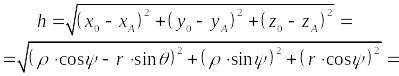
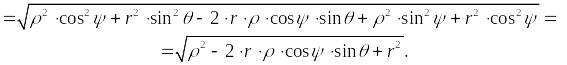
Оскільки , доданком нехтуємо

.

Враховуємо, що ,

.

Елементарний потенціал

або, нехтуючи доданкам в знаменнику

.

Сумарний потенціал

.

Використовуємо табличний інтеграл

– функція Бесселя 0-го порядку,|ладу|

.

Врахуємо, що ( – функція Бесселя 1-го порядку|ладу|),

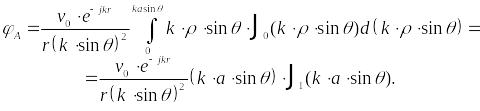
З|із| врахуванням |урахуванням|, перепишемо у вигляді|виді|

,таким чином, розділивши на

, одержимо|отримаємо|

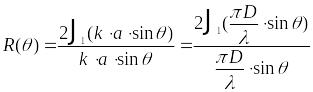
або , де

( – діаметр випромінювача).

Вид функції (значення нулів вказані приблизно):

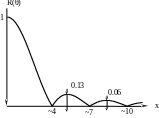
Характеристика направленості круглого поршня нагадує ХН| лінійного суцільного випромінювача.