24 Статически неопределимые балки.

К статически неопределимым балкам относятся такие балки, у которых количество неизвестных реакций связей превышает число возможных уравнений равновесия.

Подобные связи и их реакции принято называть “лишними”. Их нельзя определить методами теоретической механики.

Реакции “лишних” связей могут быть определены только методами сопротивления материалов, т. е. с использованием перемещений.

Раскрытие статически неопределимых балок производятся следующим образом:

1. Cоставляются все возможные уравнения равновесия, для балки указываются реакции.

2. Выбирается основная система (план деформаций с применением гипотезы суперпозиции).

3. По основной системе составляется уравнение деформаций.

4. Уравнение деформаций с помощью универсального уравнения упругой линии преобразуется в уравнение сил.

5) Уравнение сил решается совместно с уравнением равновесия.

25 Раскрытие статической неопределимости

однопролетной балки.

∑y=0

∑z=0

∑m=0

M_A-? R_A-? R_B-?

Задача 1 раз статически неопределима.

За лишнюю связь можно выбрать R_B, либо заделку заменить неподвижным шарниром.

а) у_Rв = у_F уравнение деформаций

б) у_в(М_a) = у_в(F)

26 Расчет 2-х пролетной статически неопределимой балки.

∑y=0

∑M=0

R_A-? R_B-? R_C-?

В данной балке за “лишнюю связь” можно принимать любую связь А,В,С.

Принимаем R_B “лишнюю связь”.

У_B(Rв) = У_B(F) уравнение деформации

Уравнение приравниваем к уравнению и находим .

27 Многопролетная балка.

Раскрытие статической неопределимости.

Рис.1 Построение эпюр Q, M, y.

При стандартных условиях равновесия

ΣY=0;

ΣM=0.

Неизвестными величинами являются R1,R2, R3 , т.е. неизвестных величин может быть сколько угодно.

Для решения этой балки сначала в общем виде строятся эпюры М и Q, а затем строится эпюра “y”. Из этих эпюр видно, что моменты инерции слева и справа от каждой опоры равны.

Θ1л = Θ1п, Θ2л = Θ2п, Θ3л = Θ3п и т.д.

М1л = М1п, М2л = М2п, М3л = М3п и т.д.

На основании записанных равенств составляется основная система (план деформаций).

На плане деформаций заданная многопролетная балка разрезается по опорам на однопролетные балки. Берется пролет балки и рисуется дважды, к первому прикладывается сила, а ко второму моменты.

Рис.2 План деформаций.

При этом моменты неизвестны. Прогибы на балках 1 и 2 должны строго соответствовать, т.е.

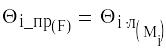
-Уравнения деформаций.

По гипотезе суперпозиций.

28 Балка, лежащая на упругом основании.

К балкам на упругом основании относятся ленточные фундаменты в здании, шпалы рельс, лыжа на снегу, корабль на воде, самолет и др.

Уравнение равновесия для такой балки.

ΣY=0

ΣRосн.-? qz осн -? - неизвестные.

Без труда определяется суммарная реакция основания.

ΣRосн = Fi

Для того чтобы определить q_z , немецкий инженер Винклер и русский инженер Фусс предложили в начале 19 века находить q_z следующим образом:

q_z = k· y_z - гипотеза Винклера.

где, k- коэффициент постели, характеризующий физико-механические свойства основания.

q_z - интенсивность давления основания.

y_z - прогиб балки в произвольном сечении.

Т. к. балка на упругом основании изгибается, то к ней применимо дифференциальное уравнение изогнутой оси балки.

y”EI = -M - дифференцируем это уравнение дважды.

y”’EI = -M’ = -Q

y^IVEI = -M” = -Q’ = - q_z = - k · y_z - дифференциальное уравнение изогнутой балки,

лежащей на упругом основании.

перепишем это уравнение.

. заменим на β⁴

. после интегрирования получим.

y_z = e ^βz (A·sinβz + B·cosβz)+ e^-βz(C·sinβz + D·cosβz). где

y_z - прогиб балки по оси Z в произвольном сечении.

Z – координата.

A, B, C, D – постоянные интегрирования, которые определяются из начальных условий для каждой конкретной балки в отдельности.

Таким образом, нахождение q_z сводится к уравнению.

q_z = k ·[ e ^βz (A·sinβz + B·cosβz)+ e^-βz(C·sinβz + D·cosβz) ] .