22 Энергетический метод определения перемещений в балках (интеграл Мора, Правило Верещагина).

Этот метод очень удобен, если не нужно строить упругую линию, а только необходимо определить прогиб в каком-то определённом сечении балки.

Суть энергетического метода проста: потенциальная энергия балки всегда равна работе деформации балки.

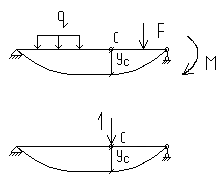
Рассмотрим балку, загруженную любыми нагрузками q, F, и т. д. Предположим, что в точке С надо определить прогиб.

Чтобы найти У_с нужно все силы, приложенные к балке, заменить единичной силой.

- интеграл Мора

Интеграл ,где

А - площадь эпюры изгибающих моментов

Yц.т. - координата У на эпюре единичных моментов под ц.т. эпюры моментов сил.

Пример 1.

Пример 2.

23 Определение прогибов в балках переменного сечения (переменной жесткости).

К балкам переменной жесткости относятся рессоры транспортных средств и конструктивные элементы экономичного веса.

Предположим, что нас интересует сечение z шириной b.

у^"ЕI_x= -М

М_x(z)= -F_z

Подставив в уравнение, получим

- ДУ изогнутой оси балки переменного сечения.

Чтобы найти прогиб, нужно интегрировать это выражение.

(рад)

(дл.)

С и D – постоянные интегрирования, которые определяются из граничных условий.

При z= ℓ Ө=0 – первое условие

у=0 – второе условие

Ө=0, тогда

Из второго условия находим D.

Подставляя С и D в уравнение, получим

Задавая z в пределах 0 ≤ z ≤ℓ можем определять прогиб в любом сечении балки.