9 Рациональные балки.

Рациональность может быть

-технической

-экономической

К технической рациональности относят:

-максимальную грузоподъёмность,

-надёжность,

-экономичность.

К экономической рациональности относят:

-минимальную материалоёмкость,

-максимальную долговечность

-минимальные трудозатраты.

а) Рассмотрим рациональные сечения балки:

Все материалы подразделяются на упругопластические и хрупкие

- упругопластический материал.

- хрупкий материал.

Поперечное сечение балок должно удовлетворять этим свойствам и соответствовать эпюрам нормальных и касательных напряжений.

1.Возьмем прямоугольное сечение балки. В этом сечении действует момент Мх и сила Q. Тогда ясно, что в этом сечении будут .

Еще есть касательное напряжение, но

И распределяется симметрично.

Двутавр является рациональным сечением для растяжения, сжатия.

2. Если материал не одинаково сопротивляется растяжению, сжатию.

Центр тяжести сечения нужно перенести вниз, для этого надо квадрат преобразовать в треугольник. Экономия материала.

б) Рациональная балка по длине.

Чтобы балка была рациональна, необходимо, чтобы касательное и нормальное напряжения были равны.

0 ≤ h ≤ h_max

На расстоянии Z определяем максимальное значение.

Если , то

Если , то

Условие прочности по касательным напряжениям:

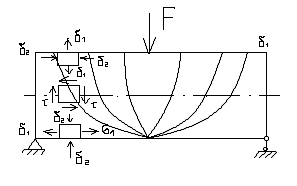
10 Траектории главных напряжений при изгибе балки.

Под траекторией главных напряжений подразумевают линию в теле балки, касательная к которой совпадает с направлением главных напряжений

Траектории главных напряжений необходимы для решения вопросов армирования балок (т.е. превращения бетонной балки в железобетонную).

Возьмём балку, в трех точках определим направления главных напряжений.

Армируем. Для того чтобы арматура не проскользнула в бетоне, загибают концы и гофрируют.

За счет арматуры повышаются растягивающие свойства.

11 Разрушающая нагрузка на балку.

В инженерной практике очень важно знать при какой нагрузке балка разрушается.

Несущая способность балок определяется из условия прочности и равна:

Нас интересует, когда перейдет в . Нужно найти соотношение между ними.

Нагрузку приложили – балка прогнулась. Нагрузку убрали – балка приняла прежнее положение.

Fразр - когда балка согнулась и не приняла прежнее положение.

Для того чтобы согласиться с эпюрой «σ_разр », нужно идеализировать материл, для этого существует диаграмма Прандтля.

Диаграмма Прандтля.

Выберем площадку dA на расстоянии y от нейтрального слоя и действует σ.

Разрушающий момент dMразр=dA*τy*y

- cтатический момент сжатой площади.

- статический момент растягивающей площади.

Wпл -пластический момент сопротивления.