38 Совместные действия и кручения.

условие прочности по касательным напряжениям от сил

Плоское напряженное состояние

Условие прочности для плоского напряженного состояния. Для этого воспользуемся третьей теорией прочности

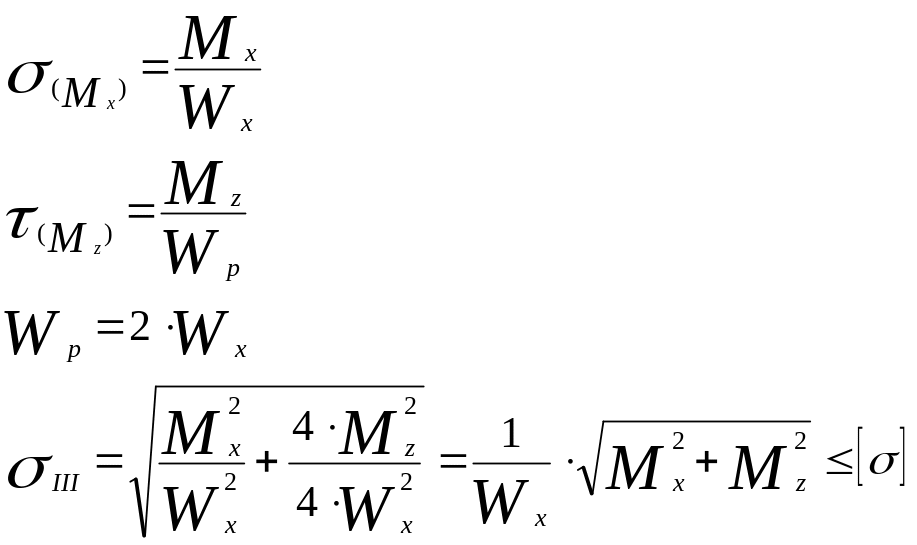
Где

39 Устойчивость сжатых стержней Общие понятия

Сопромат изучает прочность, жесткость, и устойчивость конструктивных элементов.

Прочность – это способность сопротивляться внешним нагрузкам.

Жесткость- это способность сопротивляться деформациям.

Устойчивость – способность сопротивляться изменению вида деформаций (Например, стержень должен сопротивляться появлению изгиба, изгиб сопротивляется появлению кручения и т. д.).

В общем, с философской точки зрения, под устойчивостью подразумевают, сохранение заданного состояния части системы или системы в целом. Например, сохранение состояния равновесия, движения, деформации, работы, жизнедеятельности и т.д. и т.п.

возмущении

(силы)

0

Состояния (деформации)

Любое состояние устойчиво до тех пор, пока возмущение не достигнет до критического ( _.). Переход к новому состоянию носит катастрофический характер, следовательно, любая потеря устойчивости чрезвычайно опасна и недопустима во всех случаях.

Условие устойчивости.

Потеря устойчивости любого конструктивного элемента происходит при критической силе _.→ max нагрузка на конструкцию должна быть меньше F_кр..

≤ ;

где - коэффициент устойчивости (коэффициент сжимающей нагрузки или напряжения).

0≤ ≤1;

В результате чего мы можем получить условие устойчивости по напряжениям

= ;

=0;

От силы перейдем к нормальным напряжениям, разделив силу F на площадь сечения А:

;

;

_{при сжатии} ;

σ_max=

Таким образом, мы можем получить условие устойчивости по нормальным напряжениям:

;

;

Коэффициент устойчивости ( в полученных условиях устойчивости по напряжению и силе выбирать не возможно.

40 Определение критической силы (формула Эйлера).

Определим , когда одно состояние (деформация) катастрофически сменяется другим состоянием (деформацией).

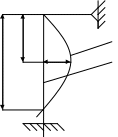
z изогнутая

у прямая

-

дифференциальное уравнение изогнутой оси балки

M =F_kp.

- дифференциальное уравнение стержня потерявшего устойчивость

где у - прогиб при потери устойчивости;

А, В – постоянные интегрирования;

z - расстояние, где определяется прогиб.

Если z=0, то у=0, В=0

Если z=l y=0

A≠0 sinCl=0 это возможно, когда

Cl=π=2π=…..=nπ (n=1,2,3,….)

формула Эйлера

n

=1, I=min

• формула Эйлера для инженерных расчетов

F_kp. прямо пропорциональна моменту инерции I и обратно пропорциональна длине l.

Для увеличения критической силы нужно увеличивать момент инерции или уменьшать длину стержня.

y

х

х

А=cons’t, I_min увеличивается, следовательно, F_kp.увеличивается.