5. Взаимное положение прямых в пространстве. Параллельные прямые.

Параллельные прямые - это прямые , лежащие в одной плоскости и никогда не пересекающиеся , сколько бы их не продлевали.  Параллельные прямые имеют параллельные одноименные проекции. Обычно по двум проекциям пары прямых можно сделать заключение о их параллельности,  однако если эти две прямые параллельны профильной плоскости проекций , то без рассмотрения третьей проекции прямых ничего утверждать нельзя

Пересекающиеся прямые.

Это прямые лежащие в одной плоскости и имеющие одну точку пересечения. Линии пересекающиеся в пространстве проектируются в виде пересекающихся проекций, причем проекции точки пересечения будут лежать на одной линии связи перпендикулярной оси Х.

Скрещивающиеся прямые.

Это прямые не параллельные и не пресекающиеся между собой. Эти прямые не имеют общей точки и не лежат в одной плоскости.

6. Способы задания плоскости на чертеже.

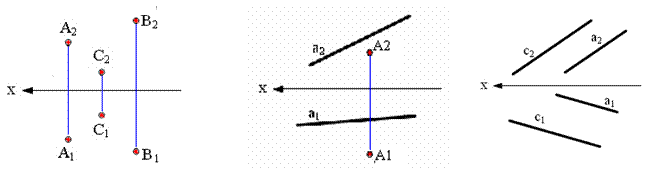
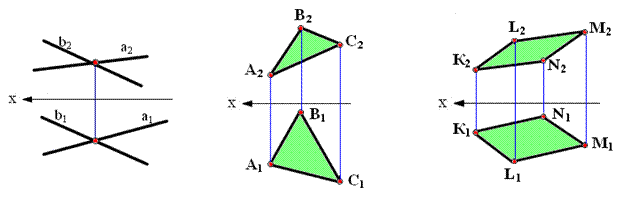
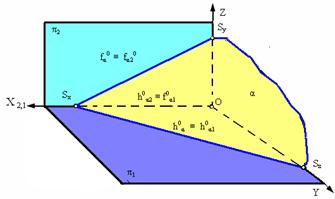
Рис. 2.12. Способы задания  плоскости:

а - тремя точками, не лежащими на одной прямой; б - прямой и точкой вне ее; в - двумя пересекающимися прямыми; г - двумя параллельными прямыми; д,е - плоской фигурой;  ж - следами плоскости

6. Прямые особого положения в плоскости. Не повезло не нашел

8. Построение линии пересечения двух плоскостей.

Две плоскости пересекаются по прямой линии. Для построения линии их пересечения необходимо найти две точки, принадлежащие этой линии. Задача упрощается, если одна из пересекающихся плоскостей занимает частное положение. В этом случае ее вырожденная проекция включает в себя проекцию линии пересечения плоскостей. Линию пересечения двух плоскостей, занимающих общее положение, можно построить в исходной системе плоскостей проекции. Для этого дважды решают задачу на построение прямой одной плоскости со второй плоскостью. Задачу можно решать в новой системе плоскостей проекции, построив изображение одной из пересекающихся плоскостей как плоскости проецирующей

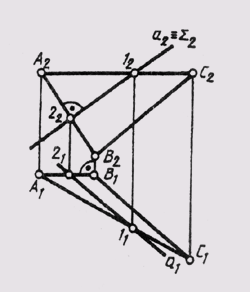
9.Построение прямой линии и плоскости параллельных между собой.

Тоже жопа.

10. Построение взаимно перпендикулярных прямой и плоскости.

Построение чертежа взаимно параллельных прямой и плоскости основано на теореме стереометрии: если прямая параллельна какой-либо прямой, принадлежащей плоскости, то данные прямая и плоскость параллельны. Пусть требуется через точку М провести прямую, параллельную плоскости Г(АВС). Для этого достаточно провести через точку М прямую l, параллельную какой-либо прямой, принадлежащей плоскости треугольника АВС. На чертеже (рис. 4.6) через точку М проведена прямая 1, параллельная CK: l₁   (С₁К₁) и l₂   (С₂К₂). 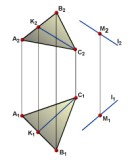 Рис. 4.6 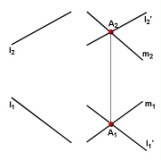 Рис. 4.7

Обратная задача - построение плоскости, параллельной данной прямой - выполняется на основании той же теоремы стереометрии. Плоскость Г(l'   m) параллельна прямой l (рис. 4.7), так как l'   Г и l   l'. Обе задачи, очевидно, имеют бесчисленное множество решений.

11. Построение взаимно перпендикулярных плоскостей.

Если плоскость проходит через прямую линию, перпендикулярную к другой плоскости (или параллельна этой прямой), то она перпендикулярна к этой плоскости. Следовательно, плоскость  , перпендикулярную данной плоскости  , можно построить:

1) либо как плоскость, проходящую через прямую, перпендикулярную плоскости  ; 2) либо как плоскость, перпендикулярную одной из прямых, принадлежащих плоскости  .

В обоих случаях задача имеет бесчисленное множество решений, если на плоскость   не наложено каких-либо дополнительных условий.