Дифракционная решетка.
Д
ифракционная
решетка – это спектральный прибор для
изучения спектрального состава света.
Она представляет собой совокупность
большого числа параллельных щелей в
непрозрачном экране или отражающих
полосок (штрихов), расположенных
параллельно друг другу на одинаковом
расстоянии.
- ширина одной щели;
- расстояние между центрами
щелей – период решетки (число штрихов
на 1 мм);
- общее число щелей.
Пусть
падающая волна монохроматическая, и ее
падение нормальное. Положение точки
наблюдения
на экране описывается углом дифракции
.
Чтобы рассчитать интенсивность в точке
,
надо просуммировать интенсивности от
всех щелей.
Комплексная
амплитуда от 1-ой щели, в предположении,
что фаза колебаний от центра 1-ой щели
в точке
равна нулю, запишется так
,
где
.
Если
за начало отсчета фазы взять фазу
колебаний, приходящую от центра 1-ой
щели в точку
,
то амплитуда от n-ой щели
запишется так
,
где
.
Полная амплитуда:
.
,
.
Здесь
,
Согласно формулам Эйлера
.
- фазовый
множитель,
- щелевой
параметр (щелевой
фактор),
- решетчатый
фактор.
Зависимость
интенсивности в точке
от ее расположения следующая
Посчитаем
интенсивность в центре, для этого
раскроем неопределенность вида
по правилу Лапиталя
.
Интенсивность равна нулю, когда щелевой множитель равен нулю
.
Побочные минимумы возникают, когда решетчатый фактор равен нулю
.
Условие
главных максимумов:
.
Между двумя главными максимумами существуют очень маленькие побочные максимумы. Между главными максимумами их
Для одной щели:
.
Щелевой график.
Нулевой
максимум:
.
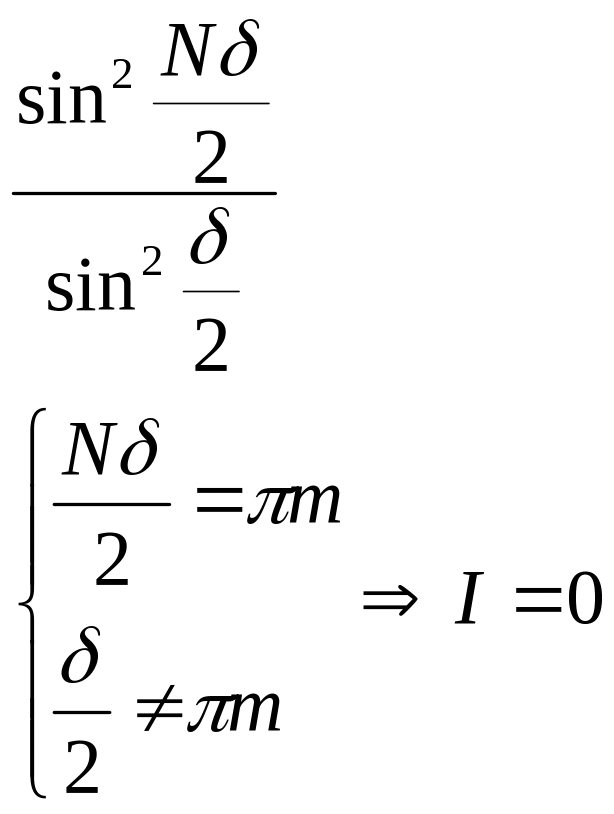
Пусть
.
Нули функции .
Побочных
максимумов –
.
С
увеличением
главные максимумы растут, и побочных
становится все больше и больше, их ширина
становиться все уже и уже, высота все
меньше и меньше.
Дифракционную решетку можно сделать и так.
Чем
шире щель, тем уже график, чем уже щель,
тем шире график.
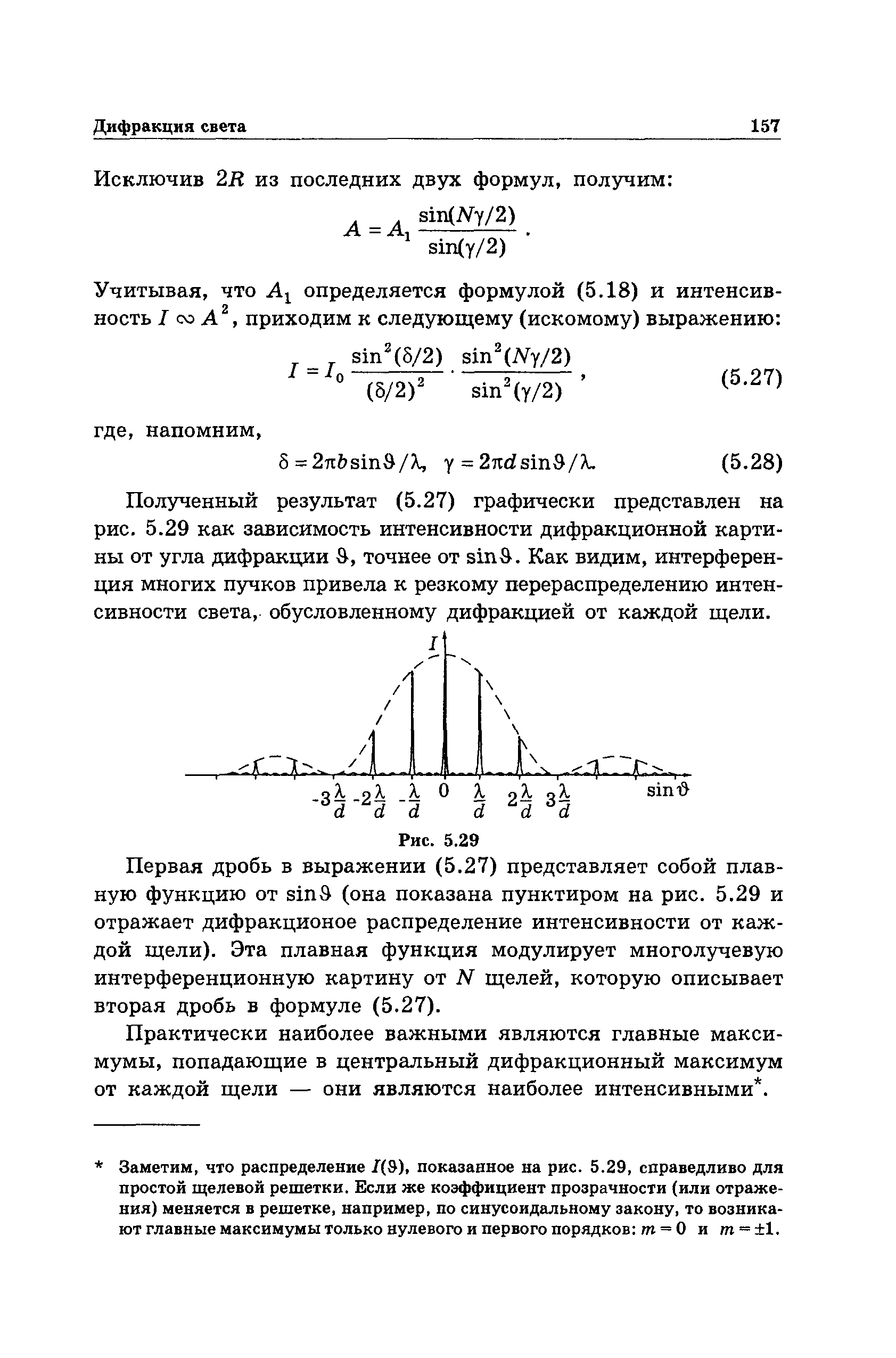
Дифракционная решетка как спектральный прибор.
Синусы
обращаются одновременно в ноль, когда
.
Угловая
дисперсия
.
Дисперсионная
область
.
Разрешающая
способность дифракционной решетки
.
– минимальное расстояние по
,
которое можно разрешить у данной решетки.
определяется из условия Рэлея: две линии считаются разрешенными, если максимум одной длины волны – главный максимум, а максимум другой длины волны попал в первый побочный от первой.
Запишем условие главного максимума.
Кристалл как дифракционная решетка.
Вся дифракция Фраунгофера возникает внутри первой зоны Френеля.
Кристаллическая решетка – упорядоченная совокупность атомов.
Электроны взаимодействуют с переменным электромагнитным полем, они излучают.
находиться в области длины
когерентности. Волны – когерентные,
они интерферируют. Дифрагировать будут
волны с длиной волны порядка ангстрема.
Это рентгеновские волны. Это открытие
было сделано в 1914 году М. Лауэ. Это
первое доказательство атомного строения
материи.
www.testent.ru – Ваш выбор