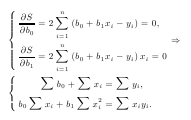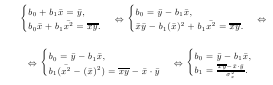shpory_po_tvims
.docx1. Случайные события. Действия над событиями. Пусть в опыте со случайным исходом имеется множество Ω (омега) всех возможных исходов опыта. Каждый элемент этого множества Е∈ Ω называют элементарным событием (исходом), само множество Ω - пространством элементарных событий (исходов). Случайным событием A в теоретико-множественной трактовке называется некоторое подмножество множества Ω : A ⊆ Ω. B свою очередь событие A может распадаться на элементарные события (непересекающиеся). Случайные события обозначаются большими латинскими буквами, а числа маленькими латинскими буквами. Множества событий обозначаются греческими буквами. Дадим определения действиям над событиями: 1. Если при появлении события B происходит и событие A, то говорят,что событие В влечет за собой событие А (или B является частным случаем
A) и обозначают B ⊂
A.
2. Если А 3. Событие, состоящее в том, что появится хотя бы одно из событий А или В называют суммой событий и обозначается А+В. 4. Событие, состоящее в том, что события А и В появятся одновременно, называется произведением событий и обозначается А*В. 5. Событие, состоящее в том, что А произойдет, а В не произойдет, называется разностью: А-В. 6. Событие называется достоверным, если оно с необходимостью (точно) происходит, и обозначается Ω (омега). 7. Событие называется невозможным, если оно не может произойти, и обозначается Ø. 8.
События А и В называются несовместными,
если их одновременное появление
невозможно 9.Событие,
состоящее в том, что А не произойдёт,
называется противоположным,
обозн.
10. События В1, ..., Вn образуют полную группу несовместных событий, если их сумма представляет все пространство элементарных событий, а сами события несовместны:
|
2. Классическое опред. вероятности и ее св-ва.
Классической
вероятностью
называется отношение числа несовместных
равновероятных событий, составляющих
А, к общему числу элементарных событий
(или отношение числа исходов m,
благоприятствующих наступлению
события А, к общему числу n
элементарных исходов испытания): Формула классической вероятности позволяет решать ограниченное число задач: 1) число элементарных событий конечно, 2) все элементарные событий равновозможны. Теория вероятности пользуется языком теории множеств, т.е. события это множества, а действия над событиями – действия над множествами. Случайные события обозначаются большими латинскими буквами, а числа маленькими латинскими буквами. Множества событий обозначаются греческими буквами. Свойства классической вероятности: 1. Вероятность невозможного события равна нулю P(∅) = 0. 2. Вероятность противоположного события равна P(A) = 1 − P(A). Р(А) +Р(А)=1. 3. Если событие A влечет за собой событие B, то P(A) ≤ P(B). 4. Для любого события A вероятность есть число, лежащее в границах от 0 до 1: 0 ≤ P(A) ≤ 1. 5. Для двух произвольных событий A и B вероятность суммы событий не превосходит суммы вероятностей P(A + B) ≤ P(A) + P(B). |
3. Аксиоматическое определение вероятности. Рассмотрим некоторое подмножество F случайных событий, причем операции сложения, умножения и вычитания не выводят из F. Числовая функция P:F→R называется вероятностью, если выполнены следующие три аксиомы: Аксиома 1. Каждому случайному событию А из F ставится в соответствие неотрицательное число, называемое вероятностью события P(A). Аксиома
2. Вероятность
достоверного события равна 1.
Аксиома 3 (аксиома сложения). Если А и В несовместные события из F, т.е. AB = ∅, то P(A + B) = P(A) + P(B). Э вероятностей этих событий. Эту аксиому называют теоремой сложения или правилом сложения вероятностей.
|
4. Формулы комбинаторики. Гипергеометрическое распределение. Комбинаторика- раздел математики, в котором изучаются задачи выбора элементов из заданного множества и расположения их в группы по заданным правилам, в частности о подсчете числа комбинаций, получаемых из элементов заданного конечного множества. Существуют две схемы выбора: схема выбора без возвращения элементов и схема выбора с возвращением элементов. Рассмотрим сначала схему выбора без возвращений. Пусть дано множество, состоящее из n различных элементов. Перестановками называются комбинации, составленные из одних и тех же элементов, которые отличаются только порядком их следования. Число перестановок из n элементов вычисляется по формуле: Pn = n! Размещениями
называются комбинации, составленные
из n
элементов по m
(0<m<=n),
которые различаются либо составом
элементов, либо порядком их следования.
Число размещений из n
элементов по m
вычисляется по формуле: Anm
= Сочетаниями
называются комбинации, составленные
из n
элементов по m
(0<m<=n),
которые различаются только составом
элементов. Число сочетаний из n
элементов по m
вычисляется по формуле: Cnm
= 1) Сn0=1; 2) Сn1=n; 3) Cnm= Cnn-m. Урновая схема: Пусть в урне имеется N шаров, среди которых M белых, а остальные черные. Наудачу вытащили k шаров, найти вероятность того, что среди них l белых. Вероятность нах. по формуле: P(A) =ClM · C k−l N−M / CkN. Эта формула называется гипергеометрическим распределением. Схема выбора с возвращением. Если при выборе m элементов из n элементы возвращаются обратно и упорядочиваются, то говорят, что это размещения с повторениями. Размещения с повторениями могут отличаться друг от друга элементами, порядком и количеством повторений элементов. Обозначаются они Anm и вычисляются по формуле: Anm = nm. Если при выборе из n элементов по m элементы возвращаются обратно без последующего упорядочивания, то говорят, что это сочетания с повторениями. Число сочетаний с повторениями обозначается Cnm = Cm n+m−1. Пусть в множестве с n элементами есть k азличных элементов, при этом первый элемент повторяется n1 раз, второй элемент - n2 раз. . . , k-й элемент-nk раз, причем n1 + n2 + ... + nk = n. Перестановки из n элементов данного множества называют перестановками с повторениями из n элементов и обозначают: Pn(n1, n2, . . . , nk) = n! / n1! n2! . . . nk! . |
5. Условная вероятность. Независимость событий. Часто при решении задач интересует вероятность появления события A после того, как некоторое событие B уже произошло. Такую вероятность называют условной и обозначают P(A/B) и вычисляют по формуле: P(A/B) =P(AB) / P(B) , P(B) > 0. Аналогично, условная вероятность события B при условии, что событие A уже произошло, вычисляется P(B/A) = P(AB) / P(A), P(A) > 0. Теорема умножения: Вероятность произведения двух произвольных событий равна произведению вероятность одного из событий на условную вероятность второго, при условии, что первое уже произошло: P(AB) = P(A)P(B/A) = P(B)P(A/B). События A и B называются независимыми, если вероятность их произведения равна произведению вероятностей этих событий: P(AB) = P(A)P(B). Для независимых событий, получим: P(A)P(B) = P(B)P(A/B). Следовательно, для независимых событий условная и безусловная вероятности совпадают P(A/B) = P(A). |
6. Формула полной вероятности. Формула Байеса. Пусть событие А может произойти только в условиях исключающих друг д Гипотезы составляют полную группу несовместных событий с известными вероятностями появления P(H1), P(H2), . ., P(Hn), (Hi · Hj = ∅, i = j, H1 + ... + Hn = Ω). Рассматривается некоторое событие A, которое может появиться только вместе с одной из гипотез. Условные вероятности события A по каждой из гипотез заданы P(A/H1), P(A/H2), . . . , P(A/Hn). Задача состоит в том, чтобы вычислить вероятность события A. Для этого представим A как сумму n несовместных событий: A = H1A + H2A + ... + HnA =∑ HiA. По правилу сложения вероятностей несовместных событий получаем P(A) =∑P(HiA), а по правилу умножения P(HiA) = P(Hi)P(A/Hi). Откуда окончательно имеем P(A) =∑P(Hi)P(A/Hi) – формула полной вероятности. Иногда интересует, как перераспределятся вероятности гипотез после того, как событие A уже произошло: P(Hj/A) . По теореме умножения P(AHj) = P(A)P(Hj/A) = P(Hj)P(A/Hj), P(Hj/A) = P(Hj)P(A/Hj) / P(A). Подставляя в знаменатель формулу полной вероятности, получим формулу Байеса: P(Hj/A) = P(Hj)P(A/Hj) / ∑P(Hi)P(A/Hi) |
7. Схема независимых испытаний Бернулли. Пусть производиться n независимых опытов, в каждом из которых может появиться или не появиться некоторое событие A, вероятность появленния P(A) = p, а не появления P(A) = q, при этом q = 1 − p. p+q=1. Требуется найти вероятность Pn(m) того, что событие A в этих n опытах появиться ровно m раз. Под элементарным событием в схеме Бернулли будет понимать последовательность наступлений и не наступлений события A и n испытаниях. Для произвольных m и n вероятность одного элементарного исхода равна pmq n−m. Число таких элементарных исходов равно числу способов разместить m единиц по n местам, а это по определению есть число сочетаний из n элементов по m. Таким образом, формула Бернулли имеет вид Pn(m) = Cnmpmq n−m. Часто в схеме Бернулли интересует вероятность появления события A не ровно m раз, а от m1 до m2 раз включительно. Тогда она определяется формулой: Pn(m1<= m<= m2) =∑Cnmpmq n−m. |
8. Предельные теоремы в схеме Бернулли. При больших n применение формулы Бернулли затруднительно из-за сложности вычисления факториалов и степеней. В этом случае используются приближенные формулы. Рассмотрим два случая: а) p → 0 или p → 1; б) p ∈ (0,1) и не близко ни к нулю, ни к единице. Теорема Пуассона: Пусть в схеме Бернулли n → ∞, p → 0 так, что np → a, тогда Pn(m) →(am/m!)*e−a. Замечание. 1) np = a - среднее число появления события A в n испытаниях. 2) Как правило, теорему Пуассона применяют, когда a ≤ 10. 3) В книгах по теории вероятностей имеются таблицы для подсчета вероятности по формуле для различных a и m. Локальная
предельная теорема Муавра-Лапласа:
Если вероятность наступления некоторого
события A в n независимых испытаниях
постоянна и равна p, p ∈
(0,1), то вероятность того, что в этих
испытаниях событие A наступит ровно
m раз, удовлетворяет при n → ∞ соотношению
Pn(m)
→ равномерно по всем m, для которых x
=
называется плотностью нормального распределения. Интегральная предельная теорема Муавра-Лапласа: Если m есть число наступлений события в n независимых испытаниях, в каждом из которых вероятность этого события равна p причем, p∈ (0,1), то равномерно относительно a и b при n→∞ имеет место соотношение P (a ≤ ≤ b) →
Замечания:1)Ф-ция Лапласа нечетная Φ0(−x) = - Ф0(x). 2) Функция Ф0(z) асимптотическая, при х→∞ она быстро стремится к 0,5. Это стремление настолько быстрое, что при х>=5 Ф0(z) можно считать равной 0,5. 3) Плотность нормального распределения φ(x) – четная функция. 4) Функции φ(x), Ф0(z) заданы таблично. |
|
|
|
|
9. Функция распределения вероятностей и ее свойства. Случайной величиной ξ называется функция, определенная на множестве элементарных событий Ω (омега). Случайная величина является функцией элементарных исходов ω, поэтому говорят, что случайная величина-это величина, значения которой зависят от случая. Случайные величины могут быть дискретными и не дискретными. Если множество Ω счетное или конечное, то случайная величина ξ называется дискретной, если несчетное- не дискретной. Законом распределения вероятностей дискретной случайной величины ξ называют соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически и графически, обычно изобр. в виде таблицы. Пусть ξ-случайная величина и x- произвольное действительное число. Вероятность того, что ξ примет значение, меньшее чем x, называется функцией распределения вероятностей: Fξ(x) = P(ξ < x). Случайная величина называется непрерывной, если ее функция распределения F(x) непрерывна. Св-ва функции распределения: 1) ∀x ∈ R, 0 ≤ F(x) ≤ 1, так как это вероятность. 2) F(x)- неубывающая функция, то есть если x2 > x1, то F(x2) ≥F(x1). Следствия: 2.1) Вероятность попадания случайной величины в заданный интервал есть приращение функции распределения на этом интервале. Следует из P(x1 ≤ ξ < x2) = F(x2) − F(x1). 2.2) Вероятность принять одно фиксированное значение для непрерывной случайной величины равна нулю. Подставляя в x2 =x1 + ∆x, P(x1 ≤ ξ < x1 + ∆x) = F(x1 + ∆x) − F(x1) → 0, при ∆x → 0, так как функция распределения непрерывной случайной величины непрерывна. 2.3) Вероятность попадания непрерывной случайной величины в открытый или замкнутый промежуток одинакова: P(a ≤ ξ ≤ b) = P(a < ξ ≤ b) = P(a ≤ ξ < b) = P(a < ξ < b). 3) F(x) непрерывна слева в каждой точке x ∈ R.4)F(−∞) = 0. 5) F(+∞) = 1. |
10. Плотность распределения вероятностей и ее свойства. Плотностью распределения вероятностей непрерывной случайной величины ξ называется производная функции распределения: pξ(x) =dFξ(x) / dx.. Свойства функции распределения: 1◦ ∀x ∈ R, p(x) ≥ 0, так как это производная неубывающей функции. 2◦
P(x1
≤ ξ < x2)
=
3◦
F(x)
=
4◦
Свойство нормировки:
Случайная величина называется распределенной по равномерному закону, если её плотность вероятности принимает постоянное значение в пределах заданного интервала: p |
11. Математическое ожидание и его свойства. Математическим ожиданием дискретной случайной величины называется сумма произведений всех возможных её значений на вероятности этих значений Mξ = ∑xipi, если этот ряд сходится абсолютно. Если математическое ожидание равно бесконечности, то говорят, что оно не существует. Математическим ожиданием непрерывной случайной величины с плотностью вероятностей p(x) называется интеграл Mξ
= Свойства математического ожидания Mξ: 1◦ Математическое ожидание постоянной величины равно самой постоянной:MC = C= const. 2◦ Математическое ожидание суммы случайных величин равно сумме их математических ожиданий: M(ξ1 + ξ2) = Mξ1 + Mξ2. 3◦ Для независимых случайных величин ξ1 и ξ2 математическое ожидание произведения равно произведению математических ожиданий M(ξ1 · ξ2) = Mξ1 · Mξ2. Следствие. Постоянный множитель выносится за знак математического ожидания. M(Cξ1) = CM(ξ1) |
12. Дисперсия и ее свойства. Дисперсей называется математическое ожидание квадрата отклонения случайной величины ξ от своего математического ожидания: Dξ = M(ξ − Mξ)2= Mξ2 − (Mξ)2. Для дискретной случайной величины ξ с законом распределения (xi, pi) дисперсия равна Dξ =∑xi2pi – (∑xipi)2. Для непрерывной случайной величины ξ с плотностью вероятности p(x) дисперсия равна Dξ
=
Dξ
=
Средним квадратическим отклонением называется корень квадратный из дисперсии σξ
= Свойства дисперсии 1◦ Дисперсия постоянной равна нулю. DC = M(C − MC)2 = M(C − C)2 = M(0) = 0. 2◦ Для независимых случайных величин дисперсия суммы равна сумме дисперсий D(ξ1 + ξ2) = Dξ1 + Dξ2. 3◦ Если a и b=const, то D(a + bξ) = b2Dξ. В самом деле D(a + bξ) = M(a + bξ − a − bMξ)2 = M(b(ξ − Mξ))2 = b2Dξ. Следствие. Постоянный множитель выносится за знак дисперсии в квадрате D(Cξ)2 = C2Dξ. |
13.
Коэффициент
корреляции и ковариация. Ковариацией
случайных величин ξ1,
ξ2
называется математическое ожидание
произведения отклонений случайных
величин от своих математических
ожиданий cov(ξ1,
ξ2)
= M((ξ1
− Mξ1)(ξ2
− Mξ2)).
Раскрыв скобки в (2.14) по свойствам
математического ожидания, получим
cov(ξ1,ξ2) = M(ξ1ξ2)
− Mξ1Mξ2.
Свойства
ковариации: 1◦
cov(ξ1,ξ1)
= M(ξ1
− Mξ1)2
= Dξ1.
2◦ Для независимых
случайных величин ковариация равна
нулю cov(ξ1,ξ2) = M(ξ1ξ2)
− Mξ1Mξ2 = Mξ1Mξ2 − Mξ1Mξ2
= 0. Обратное не верно.
3◦ Постоянный
множитель выносится за знак ковариации.
cov(Cξ1,
ξ2)
= Ccov(ξ1,
ξ2).
4◦ |cov(ξ1, ξ2)| ≤
Коэффициентом корреляции называется ρ(ξ1,
ξ2) =
Свойства коэффициента корреляции 1◦ Коэффициент корреляции по модулю не превосходит единицы, что следует из четвёртого свойства ковариации: |ρ| ≤ 1. 2◦ Если ξ1 и ξ2 независимы, то коэффициент корреляции равен 0. Обратное не верно. Если ρ = 0, то говорят, что ξ1 и ξ2 некоррелированы. 3◦ Если ξ1 и ξ2 связаны линейной зависимостью ξ2 = aξ1+ b, то |ρ(ξ1, ξ2)| = 1. Причем, если a>0, то ρ(ξ1, ξ2)=1; если а<1, то ρ(ξ1, ξ2)= - 1. Если |ρ|<1, то говорят, что ξ1 и ξ2 связаны корреляционной зависимостью, тем более тесной, чем ближе |ρ| к 1.
|
14. Моменты.
Математ.
ожидание и дисперсия являются частными
случаями моментов случайной величины
(СВ). Начальным моментом порядка k
СВ x
называется мат. ожидание k-й
степени этой величины =M Для
дискретной случ. величины x
начальный момент: =∑xik*pi,
для непрерывной СВ: = Центральным моментом порядка k СВ называется матожидание в степени k отклонения случайной величины от своего мат. ожидания =M(ξ-Mξ)k. Например второй центральный момент это дисперсия: µ 2 = Dξ. Любой центральный момент можно выразить через начальный. Например третий центральный момент =f(μ1, …,μk).
|
15. Основные дискретные распределения случайных величин. Биномиальное распределение: Рассмотрим схему Бернулли. Производится последовательность n независимых испытаний в каждом из которых возможно только два исхода: событие A появилось с вероятностью p или событие A не появилось с вероятностью q, т. е. P(A) = p, P(A) = q, p + q = 1. Число появлений события A в серии из n независимых испытаний может принимать значения µ : 0, 1, .., m, ., n. Вероятности принять эти значения вычисляются по формуле Бернулли:Pn(µ = m) = Pn(m) = =Cnmpmqn−m. Закон распределения дискретной случайной величины, определяемой по предыдущей формуле формуле называется биномиальным. Биномиальное распределение имеет два параметра: n и p. Определим их вероятностный смысл. Для этого вычислим математическое ожидание и дисперсию. Математическое ожидание: Mµ =∑M(µi) = np. Чтобы найти дисперсию, вычислим Mµi2: Mµi2 = 02 · q + 12 · p = p. Dµi = Mµi2 − (Mµi)2 = p − p2 = p(1 − p) = pq. Так как µi независимы, то Dµ = npq, σµ = √npq. Распределение
Пуассона: Распределением
Пуассона называется распределение
вероятностей дискретной случайной
величиной ξ, определяемое формулой
P(ξ = m) = P(m) = Геометрическое распределение имеет один параметр p. Математическое ожидание и дисперсия этой случайной величины: Mξ =1 / p; Dξ =1 – p / p2. Вероятностный смысл параметра p-величина, обратная математическому ожиданию.
|
1 p(x)=
0, x⋴(a,b). Ф F(x)= 0, x≤a,
1, x>b. Равномерное распределение имеет два параметра a и b. Математическое ожидание и дисперсия: Mξ =(a + b) / 2, Dξ = (b − a)2 / 12.
П p(x)= 0, x<0, λ Показательное распределение имеет один параметр λ. Функция распреденения: F 1- Mξ=1/λ; Dξ=1/λ2; σξ=1/λ. Характерным свойством показат. распределения является равенство математического ожидания и среднеквадратического отклонения. |
|
|
22. Неравенство Чебышева. Сходимость случайных последовательностей. Для случайной величины ξ, имеющей ограниченную дисперсию Dξ, для любого ε > 0 справедливо неравенство Чебышева: P(|ξ-Mξ|≥ ε ≤ Dξ/ε2. Последовательность случайных величин ξ1, ξ2, ξn, cходится по вероятности к величине a (случайной или неслучайной), если для любого ε>0 вероятность события |ξn − a| < ε при n → ∞ стремится кдинице: lim P(|ξn − a| < ε) = 1. Сходимость по вероятности обозначается ξn→ a. |
20. Независимость случайных величин. Случайные величины Х и У называются независимыми, если независимыми являются события {Х<х} и {У<у} для любых действительных х и у. В противном случае случайные величины называются зависимыми. Теорема 1. Для того, чтобы случ. величины Х и У были независимы, необходимо и достаточно, чтобы функция распределения системы (Х,У) была равна произведению функций распределения составляющих: F(x,y)=F1(x)*F2(y). Теорема 2. Необходимым и достаточным условием независимости двух непрерывных случайных величин, образующих систему (Х,У), является равенство f(x,y)=f1(x)*f2(y). Теорема 3. Необходимым и достаточным условием независимости двух дискретных случайных величин Х и У, образующих систему, является равенство pij=pxi*pyj
|
17.
Нормальное
распределение. Нормальным (распределением
Гаусса) называют распределение
вероятностей случайной величины,
которое описывается плотностью p(x)= Нормальное распределение определяется двумя параметрами α и σ. Можно показать, что Mξ = a, Dξ = σ2, σξ = σ.
При
а=0 и σ=1 получим стандартное нормальное
распределение: φ(x)=
От
произвольного нормального распределения
можно перейти к стандартному с помощью
преобразования z=
(x-a)/σ.
Функция стандартного нормального
распределения имеет вид: Ф(х)= Функция
Лапласа: Ф0(х)= Функции Ф0(х) и Ф(х) связаны между собой соотношением Ф(х)= ½+Ф0(х). Вероятность попадания нормальной случ.величины в заданный интервал: P(α<ξ<β)=Ф0( Вероятность
заданного отклонения от математического
ожидания для нормальной случайной
величины Р(|ξ-а|<δ)=2Ф0( Правило трех сигм: Если случайная величина распределена нормально, то с вероятностью, близкой к единице, абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.
|
18. Двумерная функция распределения и ее свойства. Упорядоченная пара (Х,У) двух случ. величин Х и У назыв. двумерной случ. вел. Ф-цией распред. двум. СВ (Х,У) наз. функция F(x,y), которая для любых чисел х и у равна вероятности совместн. выполнения 2-х событий. Т.о., по определению, F(x,y)=P{X<x,Y<y}. Геометрич. ф-ция интерп. как вероятность попадания случ. точки (Х,У) в бесконечный квадрат с вершиной в т.(х,у), лежащей левее и ниже её. Ф-ция распред. двум. дискретной СВ (Х,У) наход. суммированием всех вероятностей pij для которых xi<x, yi<y, т.е. F(x,y)=∑∑pij. Св-ва двум. ф-ции распределения: 1. Ф-ция распределения F(x,y) ограничена, т.е. 0≤ F(x,y)≤1. 2. F(x,y) –неубывающая функция. 3.
4. F(+∞, +∞)=1 5. Если один из аргументов обращается в +∞, то функция распределения системы случ. величин становится ф-цией распред. СВ, соответствующей другому элементу, т.е.: F(x,+∞)=F1(x)=FX(x), F(+∞,y)=F2(y)=FY(y). 6. F(x,y) непрерывна слева по каждому из своих аргументов
|
19. Двумерная плотность вероятности и ее свойства. Двумерная случайная величина называется непрерывной, если её ф-ция распределения F(x,y) есть непрерывная ф-ция, дифференцируемая по каждому из аргументов, у которой существует вторая смешанная производная F’’xy(x,y). Плотность распределения вероятностей непрерывной двумерной СВ называется вторая смешанная производная её функции распредел. Т.о.,
по определению: f(x,y)= Плотность распредел. вероятностей непрерывной двумерной СВ есть предел отношения вероятности попадания случ. точки в элементарный прямоугольник со сторонами ∆х и ∆у, примыкающей к точке (х,у), к площади этого прямоугольника, когда его размеры ∆х и ∆у стремятся к нулю. Геометрически плотность распределения вероятностей системы двух случайных величин представляет собой некоторую поверхность, называемую поверхностью распределения. Св-ва плотности распред.: 1. Плотность распределения двумерной случайной величины неотрицательна, т.е. f(x,y)≥0. 2.
Вероятность попадания случайной точки
(Х,У) в область D
равна двойному интегралу от плотности
по области D,
т.е. P{(X,Y)⋴D}= 3.
Ф-ция распределения двумерной СВ может
быть выражена через её плотность
распределения по формуле: F(x,y)= 4. Условие нормировки: двойной несобственный интеграл в бесконечных пределах от плотности вероятности двумерной СВ равен единице, т.е. =1. 5.
Плотности распределения одномерных
составляющих Х и У могут быть найдены
по формулам:
|
21. Условный закон распределения. Если случайные величины Х и У, образующие систему (Х,У), зависимы между собой, то для характеристики их зависимости вводится понятие условных законов распределения СВ. Условным законом распределения одной из случайных величин, входящей в систему (Х,У), называется её закон распределения, найденный при условии, что другая СВ приняла определенное значение. Пусть
(Х,У) – дискретная двумерная СВ и
pij=pxi*pyj
. В
соответствии с определением условных
вероятностей событий, условная
вероятность того, что СВ У примет
значение yi
при условии, чтоХ=хi
определяется
равенством p(
|
23. Теорема Чебышева. Теорема Бернулли. Теорема (Чебышева). Если ξ1, ξ2, . . ., ξn - последовательность попарно независимых случайных величин, имеющих конечные дисперсии, ограниченные одним и тем же числом C > 0, то для любого ε > 0 выполняется lim
P(| n→∞ Суть закона больших чисел: если чиcло случайных величин неограниченно растёт, то их среднее арифметическое утрачивает смысл случайной величины и стремится к постоянной величине, равной среднему арифм. их математических ожиданий. Теорема (Бернулли). Пусть в схеме испытаний Бернулли вероятность появления события A в одном испытании равна p, число наступлений этого события при n независимых испытаниях равно m, то для любого числа ε>0 lim P(|m/n − p| < ε) = 1, n→∞ то есть относительная частота w = m/n события A сходится по вероятности к вероятности p события A. |
24. Центральная предельная теорема. Центральная предельная теорема (ЦПТ). Пусть
ξ1,
ξ2,
. ., ξn
- последовательность независимых
случайных величин. Обозначим ηn
= ξ1
+ ξ2
+ ... + ξn.
Говорят, что к последовательности
ξ1,ξ2,...,ξn,...
применима ЦПТ если при n → ∞ закон
распределения ηn
стремится
к нормальному:
lim
P( Суть ЦПТ: при неограниченном увеличении числа случайных величин закон распределения их суммы стремится к нормальному. Частным случаем ЦПТ является интегральная предельная теорема Муавра-Лапласа: limPn(a≤ Сформулируем ЦПТ для одинаково распределенных случайных величин: Пусть СВ ξ1, ξ2, . . . , ξn, независимы, одинаково распределены, имеют конечные математическое ожидание Mξi = a и дисперсию Dξi = σ2. Тогда к этой последовательности применима ЦПТ: Lim
P( |
25. Выборочный метод. Пусть изучается некоторый количественный признак X и для его изучения имеется некоторая совокупность объектов. Иногда исследуются все объекты совокупности, иногда только их часть. Совокупность объектов, взятых для исследования, называется выборкой. Совокупность объектов, из которых взята выборка, называется генеральной. Число объектов (выборочной или генеральной) совокупности называется объемом. Чтобы выборка хорошо отражала генеральную совокупность, она должна быть случайной и выборочные значения должны быть независимыми. Пусть из генеральной совокупности извлечена выборка, причём x1 наблюдалось n1 раз, x2 - n2 раза, xk- nk раз и ∑ni=n –объем выборки. Наблюдаемые значения хi называются вариантами, ni их частотами. Перечень вариантов, записанных в возрастающем порядке, и соответствующих частот (относительных частот) называется статистическим распределением выборки или вариационным рядом. Относительными частотами называется отношение частоты к объему выборки: wi=ni/n.
|
26. Эмпирическая функция распределения и ее свойства. Эмпирической ф-цией распределения называется функция, определяющая для каждого значения х относительную частоту события (Х<х): Fn(x)=nx/n. В теории вероятностей ф-ция распределения генеральной совокупности называют теоретической функцией распределения. Различие между этими функциями состоит в том, что теоретическая функция F (x) определяет вероятность события (X < x), а эмпирическая функция Fn (x) относительную частоту этого события. На основании теоремы Бернулли эмпирич. ф-ция распред. стремится к теоретической. Таким образом, эмпирическая функция распределения строится для оценки вида теоретической функции распределения. Св-ва: 1. Для любого действительного числа x функция распределения заключена в интервале от 0 до 1: 0≤Fn (x)≤1. 2. Fn (x) - неубывающая функция. 3◦ Fn (x) непрерывна слева в каждой точке x ∈ R. 4◦ Если a = min{xi}, то для каждого x ≤a Fn (x) = 0. Если b = max{xi}, то для каждого x > b Fn (x) = 1. |
27. Гистограмма и полигон. Полигоном частот называют ломанную, отрезки которой соединяют точки с координатами: (x1, n1) , (x2, n2) , . ., (xk, nk) . Для изучения непрерывного признака строится гистограмма. Для этого интервала [a,b], где a=min{xi}, b=max{xi} делится на несколько частичных интервалов одинаковой длины h. Затем подсчитывается число вариантов ni попавших в каждый интервал. Гистограмма- фигура, сост.из прямоугольников, основаниями которых служат частичные интервалы длины h, а высоты равны ni/h. Тогда площадь i-го прямоугольника равна Si = h*ni/h= ni, а площадь всей гистограммы S =∑Si = n, где n- обьем выборки. Аналогично строится гистограмма относительных частот. При этом вдоль оси Oy откладываются wi/h . Тогда площадь i-го прямо- угольника равна Si = h*wi/h= wi. А площадь всей гистограммы S = ∑Si = 1. Аналогичным свойством нормировки обладает плотность распределения вероятностей. Таким образом, гистограмма относительных частот служит для оценки вида плотности вероятности. |
2 В ыборочной дисперсией называется среднее значение квадратов отклонения вариант от выборочного среднего Db = ∑(xi − xB)2 ni или Db = x2 − (xb)2; Выборочным
средним квадратическим отклонением
называется корень квадратный из
дисперсии σB
= Начальным моментом r-го порядка называется ср. знач. r-ых степеней вариант Mr = ∑xirni. Ц ентральным моментом r-го порядка называется среднее значение отклонений в степени r от среднего mr = ∑(xi − xb)r ni. Модой называется варианта, которая имеет наибольшую частоту. Медианой называется варианта, которая делит вариационный ряд на две части, равные по числу вариант. Для нормального распределения среднее значение, мода и медиана совпадают. Ассиметрией называют следующую величину As = m3 / σ3b. Пределы значений ассиметрии от −∞ до +∞. Для нормального распределения As = 0. Эксцессом называют величину Ex = (m4/σb4 )− 3. Для нормального распределения Ex = 0. |
30. Стандартная ошибка точечной оценки. Пусть θˆ - точечная оценка параметра. Стандартной ошибкой точечной оценки назыв. ср.квадратическое отклонение от оценки S=σ(θˆ). П
|
31. Доверительные интервалы. Оценка неизвестного параметра, которая задается двумя числами(концами интервала), называеться интервальной. Пусть по выборке получена точечная оценка θˆ неизвестного параметра θ. Эта оценка тем точнее, чем меньше |θ − θˆ| . Методы математической статистики не позволяют наверняка утверждать, что выполняется неравенство |θ−θˆ|< δ, где δ > 0. Можно лишь говорить о вероятности его выполнения P(|θ − θˆ|) < δ = γ. Величина γ называется доверительной вероятностью или надежно- стью. В качестве γ берут число, близкое к единице: 0,95; 0,99; 0,995. Оно выбирается исследователем самостоятельно. Раскрыв знак модуля, получим определение доверительного интервала P(θˆ− δ < θ < θˆ+ δ) = γ. Доверительным называется интервал (θˆ− δ;θˆ+ δ), который покрывает неизвестный параметр θ с заданной надежностью γ. При этом δ называется точностью оценки. Замечание. Неверно говорить, что θ попадает в интервал. Задача состоит в том, чтобы построить такой интервал, который бы заключал в себе неизвестный параметр θ. Для того, чтобы построить доверительный интервал, необходимо знать закон распределения оценки θˆ = θˆ(x1, x2, . . ., xn) как функции от выборки (x1, x2, . . ., xn). Затем поступают следующим образом: а) вычисляют точечную оценку θˆ, б) выбирают надёжность γ, в) вычисляют точность оценки δ. |
|
|||
29.
Точечное оценивание. Пусть
вид распределения изучаемого признака
X известен F(x,θ), но неизвестно значение
входящего параметра θ(тета). Задача
оценивания неизвестного параметра
θ(тета) состоит в построении приближенных
формул по выборочным данным: θˆ =∼
θˆ(x1,
x2,
. . . , xn).
Функцию θˆ =∼
θˆ(x1,x2,...,xn)
называют выборочной
функцией
или статистикой,
а её значения в приближенном равенстве
- оценкой.
Оценки
параметров подразделяются на точечные
и интервальные. Точечная
оценка параметра θ
определяется одним числом θˆ. Для того
чтобы статистическая оценка давала
хорошее приближение оцениваему
параметру θ, она должна удовлетворять
определенным требованиям: несмещенность,
состоятельность, эфективность. Оценка
θˆ называеться несмещенной,
если её математическое ожидание равно
оцениваемому параметру θ: M(θˆ) = θ.
Примером
несмещенной оценки является выборочное
среднее для математического ожидания
aˆ = xb.
Примером смещенной оценки является
выборочная дисперсия Dˆ =σb2.
Для того, чтобы получить несмещенную
оценку σ2,
вводиться понятие исправленной
выборочной дисперсии. S2
=
Оценка θˆ параметра θ называется состоятельной, если для любого ε > 0 limP(|θˆ− θ|< ε) = 1. Состоятельность оценки означает, что при большом объеме выборки оценка приближается к истинному значению параметра θ(чем больше n, тем точнее оценка). Примерами состоятельных оценок являются начальные и центральные эмпирические моменты для соответствующих теоретических моментов. Чем меньше дисперсия оценки, тем меньше вероятность ошибки при вычислении θˆ. В связи с этим целесообразно, чтобы дисперсия оценки была минимальной, то есть чтобы выполнялось условие D(θˆ(x1, . . . , xn)) = Dmin. Оценка, обладающая таким свойством, называетcя эффективной. |
32. Распределения
Распределение χ2 (хи-квадрат). Пусть ξ1,...,ξn независимы и имеют стандартное нормальное распределение. Тогда случайная величина χ2n = ξ12 + . + ξn2 называеться распределенной по закону χ2 с n степенями свободы. Математическое ожидание и дисперсия распределения χ2 равны: Mχn2 = n. Dχ2 = 2n. При n → ∞ распределение χ2 медленно стремиться к нормальному. Распределение Стьюдента. Пусть ξ1 и ξ2 независимы и ξ1 имеет стандартное нормальное распределение, а ξ2-распределение χ2 с k сте- пенями свободы. Тогда случайная величина Tk
= Распределение
Фишера.
Пусть ξ1
и ξ2
независимы и имеют распределение χ2
с k1
и k2
числом степеней свободы соответственно.
Тогда случйная величина F = свободы. Замечание. Табличные значения случайной величины Фишера всегда > 1. |
3
3.
Доверительные
интервалы для оценки математического
ожидания нормального распределения
при известном .
Пусть
изучаемый признак X имеет нормальное
распределение. Построим по выборке
(x1, x2, . xn) доверительный интервал для
оценки математического ожидания a при
заданной надежности γ. Несмещенной и
состоятельной оценкой математического
ожидания является выборочное среднее
значение aˆ = xв.
Пусть значение
параметра σ известно.
Доверительный интервал будет иметь
вид: xв
– tγ* |
3
4.
Доверительные интервалы для оценки
математического ожидания нормального
распределения при неизвестном .
Пусть
изучаемый признак X имеет нормальное
распределение. Построим по выборке
(x1, x2, . xn) доверительный интервал для
оценки математического ожидания a при
заданной надежности γ. Несмещенной и
состоятельной оценкой математического
ожидания является выборочное среднее
значение aˆ = xв.
Пусть σ
неизвестно. В
этом случае доверительный интервал
будет иметь аналогичный вид, только
вместо σ нужно подставить его оценку:
В результате доверительный интервал будет иметь вид
В этом случае tγ определяется по таблице распределения Стьюдента на основании γ и числа степеней свободы n-1. Так как при n→∞ распределение Стьюдента быстро стремится к нормальному, то при больших объемах выборки (n > 100) при нахождении tγ можно воспользоваться таблицей функции Лапласа. |
35. Проверка статистических гипотез. Статистической гипотезой называется гипотеза о виде неизвестного распределения или о параметрах известного распределения. Нулевой или основной называется выдвинутая гипотеза H0. Конкурирующей или альтернативной называется гипотеза H1, которая противоречит нулевой. Для проверки нулевой гипотезы используют специально подобранную случайную величину, точное или приближенное значение которой известно. Эту величину обозначают через χ2, если она распределена по закону «хи-квадрат», через T-по закону Стьюдента, F-по закону Фишера и так далее. Статистическим критерием называется случайная величина K,которая служит для проверки гипотезы H0. Для проверки гипотезы по данным выборки (выборок) вычисляют частные значения входящих в критерий величин, и получают наблюдаемое значение критерия Kнабл.Значения статистического критерия, при которых H0 принимают, называются областью принятия гипотезы. Значения критерия, при которых гипотезу H0 отвергают, называется критической областью. Точки,которые отделяют эти области, называют критическими. Различают левостороннюю, правостороннюю и двустороннюю критические области. Правосторонней называется критическая область, определяемая неравенством K > Kкр, Kкр > 0. Левосторонней называется критическая область, определяемая неравенством K < Kкр, Kкр < 0. Односторонней называют правостороннюю или левостороннюю критическую область. Двусторонней называется критическая область, определяемая неравенством K < K’кр, K >K’’кр. При проверке статистических гипотез возможно возникновение ошибок. Ошибка первого рода возникает, когда мы отвергаем правильную ну- левую гипотезу. Вероятность совершить ошибку первого рода называется уровнем значимости и обозначается α : P(H1/H0) = α. Ошибка второго рода возникает, когда мы отвергаем правильную гипотезу H1. Вероятность совершить ошибку второго рода обозначается β : P(H0/H1) = β. Величину ошибки первого и второго рода исследователь выбирает самостоятельно близкую к нулю: 0,01; 0,05; 0,001. Проверка статистических гипотез осуществляется следующим образом: а) по выборке вычисляется наблюдаемое значение критерия (Kнабл) ; б) если Kнабл попало в критическую область, то нулевую гипотезу отвергают, а если в область принятия гипотезы, то говорят, что нет оснований отвергнуть гипотезу H0. |
36. Построение критической области. Рассмотрим построение правосторонней критической области. Пусть вид распределения критерия K для проверки H0 известен и его плотность вероятности pk(x), если выполнима H0. Критическую точку найдем, исходя из требования, чтобы при условии справедливости нулевой гипотезы, вероятность того, что критерий K примет значение, большее Kкр, была равна принятому уровню значимости:P(K > Kкр/H0) = α. На
основании известной плотности
вероятности находим Kкр
из уравнения:
Критическую точку Kкр можно также найти, используя функцию распределения:1 − FK(Kkp) = α, так как P(K > Kкр/H0) = 1 − P(K < Kкр/H0) = α. Аналогично строится левосторонняя критическая область. Она определяеться неравенством K < Kкр, Kкр < 0. Критическую точку найдём, исходя из требования, чтобы при условии справедливости нулевой гипотезы, вероятность того, что критерий K примет значение, меньшее Kкр, была равна принятому уровню значимости: P(K < Kкр/H0) = α, или Рассмотрим построение двусторонней симметричной критической области P(|K| > Kкр/H0) = α. Пусть плотность распределения критерия K является четной функцией. Раскроем знак модуля и перейдем к односторонней (правосторонней) критической области P((K < −Kкр) + (K > Kкр)) = α. 2P(K > Kкр) = α, P(K > Kкр) =α/2.
|
3 7. Критерий согласия Пирсона. Одной из основных задач математической статистики является установление закона распределения случайной величины на основании экспериментальных данных. Критерий проверки гипотезы о предполагаемом виде распределения называется критерием согласия. Наиболее распространенным из них является критерий согласия Пирсона или критерий χ2. Пусть вид распределения изучаемого признака X неизвестен и пусть есть основание предполагать, что он распределен по некоторой функции теоретического распределения F(x). Сформулируем нулевую и альтернативную гипотезы. Пусть H0 : Fn(x) = F(x), H1 : Fn(x) = F(x). На основании данных выборки построим интервальный вариационный ряд. Для этого найдем: а) xmin,xmax и размах варьирования R = xmax − xmin. Весь интервал наблюдаемых значений X разделим на k частичных интервалов (xi,x i+1) одинаковой длины, где k можно вычислить по формуле Стержеса k = 3,32 · ln n + 1. б) Подсчитаем эмпирические частоты ni -число вариант, попавших в интервал (xi, xi+1). в) Затем вычислим вероятности pi попадания случайной величины в построенные интервалы, исходя из функции распределения F(x) pi = F(x i+1) − F(xi). Г) На основании теоремы Бернулли теоретические частоты вычислим по формуле n’i = npi. Критерий Пирсона позволяет ответить на вопрос, значимо ли различаются теоритические и эмпирические частоты. В качестве критерия проверки
нулевой гипотезы принимается величина
Число степеней свободы равно v = k−r−1, где k – число частичных интервалов выборки, r – число оцениваемых параметров. В частности, для нормального распределения оценивают 2 параметра (математические ожидание и среднее квадратическое отклонение), то есть r = 2. В этом случае v = k − 3. Проверим нулевую гипотезу, исходя из требований, что вероятность попадания критерия в правостороннюю критическую область равна принятому уровню значимости α: P(χ2 > χ2 кр) = α. Значение критерия, вычисленное по данным наблюдений, обозначим через χ2набл и сформулируем правило проверки нулевой гипотезы. Правило проверки нулевой гипотезы: Если χ2набл < χ2кр, то нет оснований отвергнуть H0, следоват., признак X распределен по з-ну F(x). Если χ2набл ≥ χ2кр, то H0 отвергаем и принимаем H1, следоват., признак X распределен по другому закону. |
38. Вычисление теоретических частот для нормального распределения. Пусть имеется выборка (x1,x2,··· ,xn) объема n, и есть основание предположить, что она имеет нормальное распределение. Для вычисления теоретических частот необходимо выполнить действия указанные ниже. 1) По данным выборки построить интервальный вариационный ряд. Для этого весь интервал наблюдаемых значений X надо разделить на k частичных интервалов (xi,xi+1) одинаковой длины. Находим максимальное и минимальное значение выборки и размах варьирования: a = xmin, b = xmax, R = b − a. Для определения количества интервалов группировки k воспользуемся формулой Стерджеса: k = 3,32 · lg n + 1. Число k округляется в сторону наибольшего целого числа. Тогда ширину частичных интервалов (xi,xi+1) находим из формулы h =R/k. Интервалы строятся таким образом, чтобы xmin и xmax входили внутрь интервалов. Для этого в качестве левой границы первого интервала можно взять число x0 = xmin – h/2, а в качестве правой границы последнего интервала x k+1 = xmax+h/2. В качестве частоты ni вариационного ряда записывают число наблюдений, попавших в каждый [xi,xi+1) промежуток. 2) Для того, чтобы получить оценки параметров математического ожидания a и среднего квадратического отклонения σ перейдем к дискретному ряду, взяв в качестве вариант ряда X середины построенных интервалов xi∗. В итоге получим последовательность равностоящих вариант и соответствующих им частот. Несмещенной оценкой математического ожидания является выборочное среднее xb, а дисперсии – исправленная выборочная дисперсия S2.
3) Сделаем преобразование стандартизации для X, перейдя к величинам:
Причем наименьшее значение z0 будем считать равным −∞, а наибольшее значение z i+1 = +∞, так как теоретическое нормально распределение принимает значения на всей числовой оси. 4) Вычислим вероятности pi попадания X в интерв. (zi,z i+1): pi = P(zi<x< z i+1) = Φ0(z i+1) − Φ0(zi).
5) Рассчитаем теоретические частоты n’i= npi. |
|
|
|
|
39. Сравнение дисперсий двух нормальных выборок. Предположим , что выборки X и Y имеют нормальное распределение с параметрами ax, σх, и ау, σy, объем выборок n и m. Два нормальных распределения совпадают, если равны их параметры. Проверим сначала гипотезу о равенстве дисперсий. Н0: σх2= σy2. Несмещенной и состоятельной оценкой теоретической дисперсии является исправленная выборочная дисперсия:
В связи с этим нулевая гипотеза примет вид: Н0: Sx2=Sy2. Для проверки нулевой гипотезы используется отношение дисперсий, где в
числителе ставится большая
из двух дисперсий. F= m находят Fкр.(α; n-1, m-1). Если Fнабл.< Fкр, то говорят, что нет оснований отвергнуть нулевую гипотезу. В этом случае дисперсии различаются не достоверно (случайно). Е сли Fнабл.> Fкр , то нулевую гипотезу отвергают и принимают конкурирующую. В этом случае дисперсии различаются достоверно. Пусть конкур. гипотеза двусторонняя Н1: Sx2=Sy2. В этом случае находят левостор. и правост. критические точки: Fкр.(α/2; n-1,m-1), Fkp(1-α/2; n-1,m-1). Если наблюдаемое значение критерия заключено в интервале между этими точками Fкр.(α/2; n-1,m-1)<Fнабл<Fkp(1-α/2; n-1,m-1), то нулевая гипотеза не отвергается. |
40. Сравнение
средних двух нормальных выборок
(критерий Стьюдента). Предположим
, что выборки X и Y имеют нормальное
распределение с параметрами ax,
σх,
и ау,
σy,
объем выборок n и m. Два нормальных
распределения совпадают, если равны
их параметры. Проверим гипотезу о
равенстве математических ожиданий:
H0
:aх=aу
при альтернативной гипотезе H1:aх≠aу.
Несмещенной и состоятельной оценкой
мат. ожидания является выборочное
среднее:
Т огда H0: x =y при альтернативной гипотезе H1:x ≠ y . Если нулевая гипотеза принимается, то говорят, что нет отклика на воздействие. Если принимается альтернативная гипотеза, то говорят, что есть отклик на воздействие, то есть два лекарства, две методики обучения, два сорта удобрения дают различный результат. Для поверки справедливости нулевой гипотезы используется случайная величина:
оценки дисперсий по выборкам X и У, n и m–их объемы соответственно. 1. Пусть дисперсии выборок равны, хотя и не известны. В этом случае при справедливости нулевой гипотезы величина T имеет распредел. Стьюдента с (n+m−2) числом степеней свободы. Проверка нулевой гипотезы осущ. след. образом. Вычисляется наблюдаемое значение критерия по формуле выше(Т). Затем по таблице критических точек распределения Стьюдента находят Tкр.(α;n+m-2) для двусторонней критич. области. Если |Тнабл.|<Ткр., то нулевую гипотезу не отвергают. В этом случае различие средних значений не достоверно (случайно). Если |Тнабл.|>Ткр.,то нулевую гипотезу отвергают и принимают конкурирующую. В этом случае различие средних значений достоверно (есть отклик на воздействие). 2. Дисперсии выборок не известны и не равны. В этом случае о виде распределения статистики T ничего не известно. Можно лишь говорить о том,
что ее распределение близко к
распределению Стьюдента с числом
степеней свободы
|
41.
Дисперсионный
анализ. Пусть
рассматр. m групп объектов X1,…,Xm,
и пусть известно, что они имеют
нормальное распределение. Предположим,
что дисперсии их одинаковы, хотя и
неизвестны (σ12=…=σ2m=σ2).
Тогда, эти группы являются однородными,
если = их мат. ожидания. Проверим нулевую
гипотезу о равенстве математических
ожиданий:
Н0:а1=…=ам,
при конкурирующей гипотезе Н1:
не все мат.ожидания равны между собой.
Несмещенной и состоят. оценкой
математического ожидания является
выборочное среднее значение:
Обозначим средние значения в группах:
Остаточная сумма квадратов отклонений:
Факторная сумма квадратов отклонений:
В результате получим SST= SSR+SSA, Построим оценку дисперсии исходя из SSA, факторная дисперсия будет иметь вид
Построим оценку дисперсии исходя из SSR, остаточная дисперсия будет иметь вид:
Проверка нулевой гипотезы осущ. след. образом. Вычисляется
наблюдаемое значение критерия по
формуле: Fнабл= Затем по таблице критических точек распред. Фишера на основании выбранного уровня значимости α и чисел степеней свободы n и m находят Fкр(α;m-1, nm-m). Если Fнабл<Fкр, то говорят, что нет оснований отвергнуть нулевую гипотезу. В этом случае различие средних значений не достоверно (случайно), нет отклика на воздействие.. Если Fнабл >.Fкр., то нулевую гипотезу отвергают и принимают конкурирующую. В этом случае средние в группах различаются достоверно, есть отклик на воздействие. Замечание 1. Если MSA<MSR , то F <1.Тогда сразу делают вывод о справедливости гипотезы H0. Замечание
2. Если объем
в группах различен и составляет ni,
то число степеней свободы остаточной
дисперсии будет равно N- m, а факторная
сумма квадратов вычисляется по формуле
Замечание 3. Если гипотеза H0 отвергается, то делается вывод о том, что не все средние равны между собой. Следующим шагом является попарное сравнение средних значений в группах. Это можно сделать с помощью критерия Стьюдента. Замечание 4. Если изучаемый признак не соответствует нормальному распределению, то необходимо применять непараметрический дисперсионный анализ. Это, например, критерий Краскела-Уоллиса, который реализован в статистических пакетах. |
42. Парная регрессия. Пусть требуется установить взаимосвязь между двумя количеств. признаками X и Y. X и Y могут быть независимы, связаны между собой функциональной либо корреляционной зависимостью. Функциональной называется зависимость между величинами X и Y, когда изменения каждого значениям X влечет изменение Y. Однако функционнальная зависимость между случайными величинами наблюдается редко, чаще имеется корреляционная зависимость. П ри корреляционной зависимости изменение каждого отдельного значения X не обязательно влечет за собой изменение значения Y ,однако изменение x приводит к изменению y. П усть имеется выборка объема n:(xi, yi),где i = 1, n. Регрессионный анализ оценивает вид функцион. зависимости между X и Y y = f(x) + ε, где ε - ошибка оценки. Чтобы установить вид зависимости строится поле корреляции. На плоскости наносятся точки с координатами (xi,yi), i = 1,n, и по расположению точек делают вывод о виде зависимости. Предположим, что зависимость между X и Y линейная: y = b0 + b1x + ε. Коэффициенты b0 и b1 найдем по методу наим. квадратов. Найдем b0 и b1 такие, при которых функция S достигает минимума.
Перейдем к средним значениям, поделив почленно эти уравнения на n.
Уравнение вида yˆ = b0 + b1x называется уравнением линейной регрессии Y на X. Угловой коэффициент b1 прямой называется коэффициентом регрессии. |
43. Парный коэффициент корреляции, его свойства. Выборочным коэффициентом корреляции признаков X и Y называется величина:
Квадрат коэффициента корреляции называется коэффициентом детерминации D = rв2. Св-ва выборочного коэффициента корреляции: 1◦ |rв| ≤ 1 2◦ Если X и Y независимы, то коэф. коррел.= 0. 3◦ Если X и Y связаны линейной функциональной зависимостью y =b0 + b1x, то |rв| = 1, причем при b1 > 0 r = 1, при b1 < 0 r = −1. Если |rв| < 1, то говорят, что X и Y связаны корреляционной зависимостью, тем более тесной, чем ближе |rв| к 1. Коэф. корреляции служит для колич. характер. зависимости между изуч. признаками. Коэф. детерм. пок., какая доля дисперсии признака Y обусловлена дисперсией признака X. |
|
|
|
4 4. Проверка гипотезы о достоверности выборочного коэффициента корреляции. Характеристикой корреляционной зависимости между признаками X и Y генеральной совокупн. является коэффициент корреляции rв. Рассмотрим проверку гипотезы о значимости выборочного коэффициента корреляции. Пусть по выборке объема n найден выборочный коэффициент корреляции, причем rв=0. Но это ещё не означает, что коэфф. корреляции генеральной совокупности rген будет также отличаться от нуля. Проверим нулевую гипотезу H0 о равенстве нулю коэффициента корреляции генеральной совокупности H0 : rген = 0 при конкурирующей гипотезе H1 : rген = 0. Если нулевая гипотеза будет отклонена, то это будет означать, что коэффициент корреляции значимо отличается от нуля, а X и Y коррелированны, то есть связаны линейной корреляционной зависимостью. Если будет принята, то величины не связаны линейной зависимостью. Правило проверки нулевой гипотезы: Для проверки надо вычислить наблюдаемое значение критерия
затем по заданному уровню значимости α и числу степеней свободы ν = n − 2 по таблице критических точек распределения Стьюдента найти критическую точку Tкр(α,ν) для двусторонней критической области. Если |Tнаб| < Tкр, то оснований для отклонения нулевой гипотезы нет. В этом случае выборочный коэффициент корреляции недостоверно отличент от нуля, и между X и Y нет корреляц. зависимости. Если |Tнаб| > Tкр - нулевую гипотезу отклоняют. В этом случае выборочный коэффициент корреляции достоверно отличен от нуля, X и Y связаны корреляционной зависимостью.
|
|
|
|

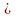 B
и В
А,
то говорят, что события А и В равновозможны
и обозначают А=В.
B
и В
А,
то говорят, что события А и В равновозможны
и обозначают А=В. Ø.
Ø.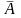 События
А
и
называются
противоположными,
если их одновременное появление
невозможно и в сумме они дают пространство
элементарных событий
События
А
и
называются
противоположными,
если их одновременное появление
невозможно и в сумме они дают пространство
элементарных событий
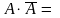 Ø,
Ø,
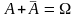 .
. Ø,
Ø,
 .
.
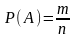 .
.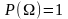
 та
аксиома легко обобщается с помощью
сочетательного свойства сложения на
любое конечное число событий. Если
AiAj
= ∅
при i = j, то Р(∑Аi
)=∑Р(Аj),
т.е. вероятность суммы попарно
несовместных событий равна сумме
та
аксиома легко обобщается с помощью
сочетательного свойства сложения на
любое конечное число событий. Если
AiAj
= ∅
при i = j, то Р(∑Аi
)=∑Р(Аj),
т.е. вероятность суммы попарно
несовместных событий равна сумме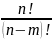
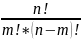 .
Св-ва сочетаний:
.
Св-ва сочетаний:
 руга
гипотез: H1,
H2,
. . . , Hn
(HiHj
= ∅
при i = j.
руга
гипотез: H1,
H2,
. . . , Hn
(HiHj
= ∅
при i = j.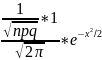 =
=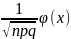
 находится
в каком-то конечном интервале; Функция
φ(x) =
находится
в каком-то конечном интервале; Функция
φ(x) =
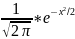
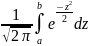 =
Φ0(b)
− Φ0(a),
где Ф0(х)=
=
Φ0(b)
− Φ0(a),
где Ф0(х)=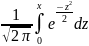 - функция Лапласа.
- функция Лапласа.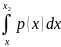 ,
P(x1
≤ ξ < x2)
= F(x2) − F(x1) =
,
P(x1
≤ ξ < x2)
= F(x2) − F(x1) =
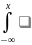 p(y)dy.
Следует из определения функции
распределения и свойства 2.
p(y)dy.
Следует из определения функции
распределения и свойства 2.
 (x)
= c=
const,
x∈(a,b)
и 0, x
∈(a,b).
(x)
= c=
const,
x∈(a,b)
и 0, x
∈(a,b).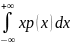 , если он сходится абсолютно.
, если он сходится абсолютно.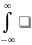 (x
− Mξ)2p(x)dx,
или
(x
− Mξ)2p(x)dx,
или
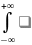 x2p(x)dx
– (
xp(x)dx)2
.
x2p(x)dx
– (
xp(x)dx)2
.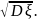
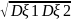
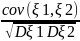 = cov(ξ1, ξ2) / σξ1σξ2.
= cov(ξ1, ξ2) / σξ1σξ2.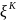 .
. .
.
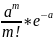 m
: 0, 1, 2,m,
где а-параметр распределения Пуассона.
Характерным св-вом распределения
Пуассона является равенство
математического ожидания и дисперсии
параметру a: Mξ = a, Dξ = a.
Геометрическое
распределение: Геометрическим
распределением называется распределение
дискретной случайной величины ξ,
определяемое формулой: Pm
= qm−1p.
m
: 0, 1, 2,m,
где а-параметр распределения Пуассона.
Характерным св-вом распределения
Пуассона является равенство
математического ожидания и дисперсии
параметру a: Mξ = a, Dξ = a.
Геометрическое
распределение: Геометрическим
распределением называется распределение
дискретной случайной величины ξ,
определяемое формулой: Pm
= qm−1p.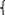 6.
Равномерное и показательное
распределения. Плотность
распределения:
6.
Равномерное и показательное
распределения. Плотность
распределения: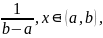
 ункция
распределения имеет вид:
ункция
распределения имеет вид:
 ,
,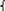 оказательным
называют распределение вероятностей
непрерывной случайной величины,
которое описывается плотностью
оказательным
называют распределение вероятностей
непрерывной случайной величины,
которое описывается плотностью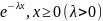
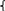 (x)=
0, x<0,
(x)=
0, x<0,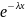 ,
x≥0.
,
x≥0.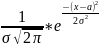 ,
σ>0.
,
σ>0. .
.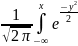 dy.
dy.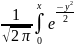 dy.
dy.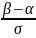 )
- Ф0
)
- Ф0
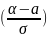 .
.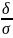 )
)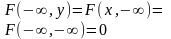
 =
F’’xy(x,y).
=
F’’xy(x,y). .
.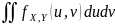
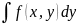 =f1(x)=fX(x).
=f1(x)=fX(x).
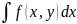 =f2(y)=fY(y)
=f2(y)=fY(y)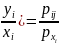 .
Совокупность вероятностей, т.е. p(
.
Совокупность вероятностей, т.е. p(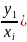 ,
p(
,
p(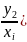 ,
…, p(
,
…, p(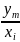 ),
представляет собой условный закон
распределения СВ У при условии Х=хi.
Сумма условных вероятностей p(
),
представляет собой условный закон
распределения СВ У при условии Х=хi.
Сумма условных вероятностей p(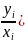 равна 1. Аналогично определяется
условная вероятность, условный закон
распределения случайной величины Х
при условии У=уi.
равна 1. Аналогично определяется
условная вероятность, условный закон
распределения случайной величины Х
при условии У=уi.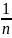 ∑ξi
-
∑Mξi|<ε)=1.
∑ξi
-
∑Mξi|<ε)=1.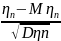 <x)
=
<x)
=
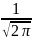
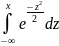 =Ф(х).
=Ф(х).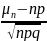 ≤b)
=
≤b)
=
 .
.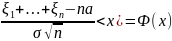
 8.
Числовые характеристики выборки.
Выборочным средним
или средним значением называется
среднее арифметическое значение
вариант xB
=
∑xini.
8.
Числовые характеристики выборки.
Выборочным средним
или средним значением называется
среднее арифметическое значение
вариант xB
=
∑xini.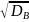 .
.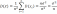 усть
ậ=х. Подсчит. её ошибку: M(xi)=a;
D(xi)=σ2.
усть
ậ=х. Подсчит. её ошибку: M(xi)=a;
D(xi)=σ2.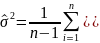
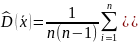
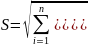
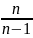 DB=
*
∑(xi-x)2.
M(S2)
=
M(DB)=σ2.
DB=
*
∑(xi-x)2.
M(S2)
=
M(DB)=σ2. ,
Стьюдента и Фишера.
,
Стьюдента и Фишера.
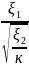 называется распределенной
по закону Стьюдента
с k
степенями свободы. При к → ∞ распределение
Стьюдента быстро стремится к нормальному.
Мат.ожидание и дисперсия распределения
Стьюдента МТ=0, DT=
называется распределенной
по закону Стьюдента
с k
степенями свободы. При к → ∞ распределение
Стьюдента быстро стремится к нормальному.
Мат.ожидание и дисперсия распределения
Стьюдента МТ=0, DT=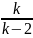 .
.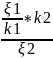 называеться распределенной
по закону Фишера
с k1
и k2
числом степеней
называеться распределенной
по закону Фишера
с k1
и k2
числом степеней <
a < xв
+ tγ
.
Здесь n- объем выборки. Точность оценки
δ = tγ
.
где значение числа tγ
находится с помощью таблиц функции
Лапласа на основании выбранной
надежности γ из уравнения 2Φ0(tγ)
= γ.
<
a < xв
+ tγ
.
Здесь n- объем выборки. Точность оценки
δ = tγ
.
где значение числа tγ
находится с помощью таблиц функции
Лапласа на основании выбранной
надежности γ из уравнения 2Φ0(tγ)
= γ.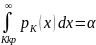
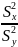 .
При справедливости нулевой гипотезы
эта случайная величина имеет
распределение Фишера с n
−1 и m
−1 числами степеней свободы. Пусть
альтернативная гипотеза одностороння
(правосторонняя). Н1:
Sx2>Sy2.
В этом случае проверка нулевой гипотезы
осуществляется следующим образом.
Вычисляется наблюдаемое значение
критерия по формуле Fнабл.=
.
Затем по таблице критических точек
распределения Фишера на основании
выбранного уровня значимости α
и чисел степеней свободы n
и
.
При справедливости нулевой гипотезы
эта случайная величина имеет
распределение Фишера с n
−1 и m
−1 числами степеней свободы. Пусть
альтернативная гипотеза одностороння
(правосторонняя). Н1:
Sx2>Sy2.
В этом случае проверка нулевой гипотезы
осуществляется следующим образом.
Вычисляется наблюдаемое значение
критерия по формуле Fнабл.=
.
Затем по таблице критических точек
распределения Фишера на основании
выбранного уровня значимости α
и чисел степеней свободы n
и
 .
.