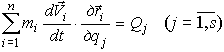20!!!!!! Уравнение Лагранжа 2го рода.
Дифференциальные уравнения движения системы в обобщенных координатах или уравнения Лагранжа второго рода.
Для вывода уравнений запишем принцип Даламбера-Лагранжа в обобщенных координатах в виде -Qju = Qj (j = 1 ÷ s).
Принимая во внимание, что Фi = -miai = -midVi / dt, получаем
|
(1) |
Далее обобщенные силы инерции в левой части нужно выразить через кинетическую энергию. Это впервые сделал Лагранж, который доказал, что для систем с голономными связями обобщенные силы инерции равны
|
(2) |
Подставляя (2) в (1) получаем дифференциальные уравнения движения системы в обобщенных координатах, которые названы уравнениями Лагранжа второго рода:
|
(3) |
то есть, материальная система с голономными связями описывается уравнениями Лагранжа второго рода по всем s обобщенным координатам.
Отметим важные особенности полученных уравнений.
1. Уравнения (3) - это система обыкновенных дифференциальных уравнений второго порядка относительно s неизвестных функций qj(t), полностью определяющих движение системы.
2. Число уравнений равно числу степеней свободы, то есть движение любой голономной системы описывается наименьшим числом уравнений.
3. В уравнения (3) не нужно включать реакции идеальных связей, что позволяет, находя закон движения несвободной системы, выбором обобщенных координат исключить задачу определения неизвестных реакций связей.
4. Уравнения Лагранжа второго рода позволяют указать единую последовательность действий для решения многих задач динамики, которую часто называют формализмом Лагранжа.
22.
23(!!!!!!!!!!!!!!!!!!!!!!!!!)
Теорема Донкина ------------------