2. Количество движения материальной точки и механической системы. Теорема об изменении количества движения.

Изменение количества движения точки за некоторый промежуток времени равно импульсу силы, действующему на точку в течение того же промежутка времени.

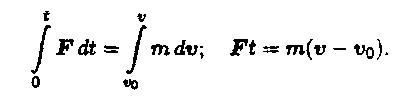
Количество движения системы равно произведению массы всей системы на скорость ее центра масс.

В инерциальной системе отсчета производная импульса материальной точки по времени равна действующей на него силе

5. Теорема об изменении кинетического момента механической системы в инерциальной системе отсчета.

Теорема об изменении кинетического момента гласит: произ-

водная по времени от кинетического момента системы относительно точки O

равна главному моменту внешних сил относительно той же точки

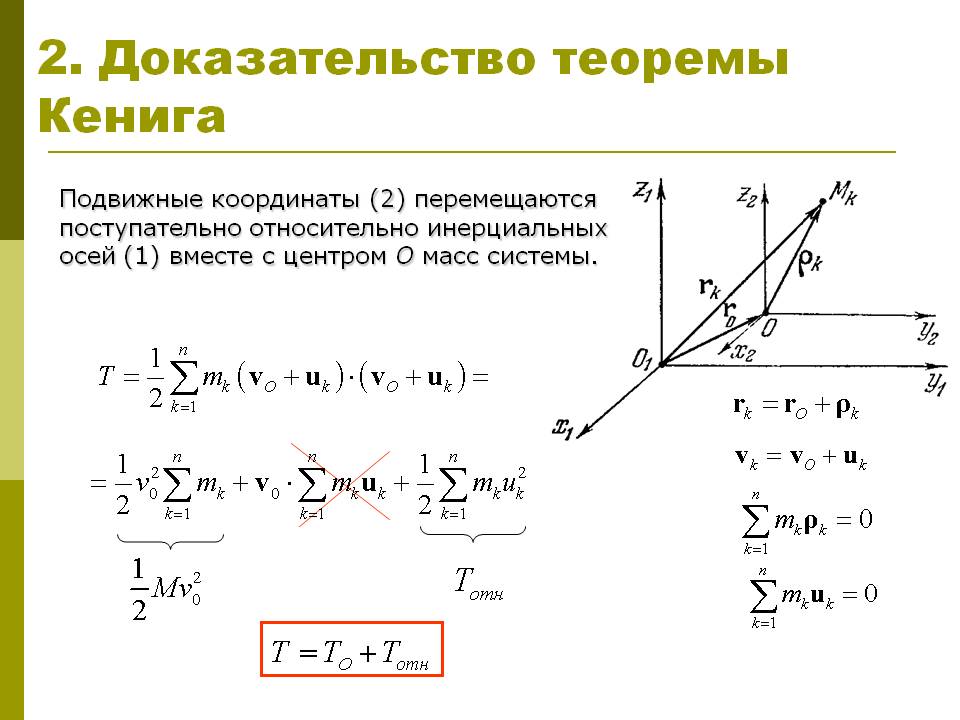
9. Теорема Кёнига. Кинетическая энергия абсолютно твердого тела.

Теорема Кёнига позволяет выразить полную кинетическую энергию системы через энергию движения центра масс и энергию движения относительно центра масс.

14. Связи классифицируются по различным признакам.

По виду ограничения различают: геометрические (интегрируемые, голо-

номные), ограничивающие перемещения ∆r , и кинематические (дифференци-

альные, неинтегрируемые, неголономные), ограничивающие скорости v.

По времени действия различают: стационарные (склерономные) связи, не

зависящие от времени, и нестационарные (реономные), зависящие от времени.

Для стационарных связей в уравнениях (2.2) исключается время – аргумент t.

По виду уравнения различают: удерживающие (двухсторонние) и неудер-

живающие (односторонние) связи. Математическая запись удерживающей свя-

зи представляется уравнением, а неудерживающая – неравенством в (2.1).

По отношению к системе различают внешние и внутренние связи.

Возможные перемещения и возможные скорости

Возможным перемещением материальной точки называется любое ее бесконечно малое перемещение , допускаемое в данный момент времени наложенными связями, а возможной скоростью точки – любая скорость точки , допускаемая в данный момент времени наложенными связями.

Возможным перемещением механической системы называется любая совокупность возможных перемещений точек данной системы, допускаемая всеми наложенными на нее связями.

Принцип возможных перемещений

Для того чтобы механическая система находилась в равновесии, необходимо и достаточно, чтобы возможная работа всех активных сил на любых возможных перемещениях была равна нулю: 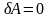или (общее уравнение статики).

Принцип возможных скоростей

Для того чтобы механическая система находилась в равновесии, необходимо и достаточно, чтобы возможная мощность всех активных сил на любых возможных скоростях была равна нулю: или .

15. Виртуальные перемещения. Вариации по Гауссу и Курдеку. Идеальные связи.

ВОЗМОЖНЫЕ ПЕРЕМЕЩЕНИЯ — (виртуальные перемещения) бесконечно малые перемещения, которые могут совершать точки механической системы из занимаемого ими в данный момент времени положения, не нарушая наложенных на систему связей

Здесь рассматривается еще один вид связей, которые называются идеальными. Связь называется идеальной, если виртуальная работа ее реакции связи равна нулю:

(14)

Если на систему наложены только идеальные связи, то алгебраическая сумма виртуальных работ реакций связей на любых виртуальных перемещениях точек системы или виртуальная работа ее реакций связей равна нулю, то есть

(15)

Можно непосредственно убедиться в том, что эти условия выполняются для известных нам типов связей. Но при изучении теоремы об изменении кинетической энергии, где используется понятие элементарной работы, мы уже доказали, что элементарная работа реакций гладких поверхностей, идеальных шарниров равна нулю. Там же мы доказали, что равны нулю работа внутренних сил абсолютно твердых тел и реакций связей, всегда приложенных в мгновенном центре скоростей.

Следовательно, к идеальным связям относятся:

a) гладкие поверхности;

b) идеальные шарниры, где моменты сопротивления малы;

с) твердые тела - нерастяжимые стержни, нити и т.д.;

d) шероховатая твердая поверхность, по которой без скольжения катится твердое тело и т.д.