Спосіб, заснований на тлумаченні інтеграла як площі.

Нехай підінтегральна функція ненегативна і обмежена: , А двовимірна випадкова величина розподілена рівномірно у прямокутнику D з підставою і висотою с.

Тоді двовимірна густина ймовірності для точок, що належать D;

поза D.

В якості оцінки інтеграла приймають ,

де n - загальне число випадкових точок   , що належать D;

- число випадкових точок, які розташовані під кривою .

Завдання. Знайти оцінку інтеграла .

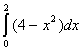Рішення. Використовуємо формулу .

В інтервалі (0,2) підінтегральна функція ненегативна і обмежена, причому ; Отже, можна прийняти c = 4.

Введемо в розгляд двовимірну випадкову величину (X, Y), розподілену рівномірно у прямокутнику D з підставою і висотою з = 4, щільність ймовірності якої .

Розігруємо n = 10 випадкових точок , Що належать прямокутнику D. Враховуючи, що складова X в інтервалі (0,2) розподілена рівномірно з щільністю і складова Y в інтервалі (0,4) розподілена рівномірно з щільністю , Розіграємо координати випадкової точки , Що належить прямокутнику D, по парі незалежних випадкових чисел : 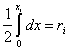, 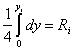. Звідси , .

Номер i
1  2  3  4  5  6  7  8  9  10	0,100  0,253  0,520  0,863  0,354  0,809  0,911  0,542  0,056  0,474	0,200  0,506  1,040  1,726  0,708  1,618  1,822  1,084  0,112  0,948	0,040  0,256  1,082  2,979  0,501  2,618  3,320  1,175  0,013  0,899	3,960  3,744  2,918  1,021  3,499  1,382  0,680  2,825  3,987  3,101	0,973  0,376  , 135  0,467  0,876  0,590  0,737  0,048  0,489  0,296	3,892  1,504  0,540  1,868  3,504  2,360  2,948  0,192  1,956  1,184	1  1  1  1  1  1

Якщо виявиться, що , То точка лежить під кривою і в «лічильник »Треба додати одиницю.

Результати десяти випробувань наведені в таблиці 3.

З таблиці 3 знаходимо .

Шукана оцінка інтеграла

Програма обчислення визначеного інтеграла методом Монте-Карло.

Обчислити визначений інтеграл 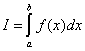за методом "Монте-Карло" за формулою

,

де n - число випробувань;

g (x) - щільність розподілу "допоміжної" випадкової величини X, причому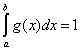 , У програмі g (x) = 1 / (ba)

Програма написана на мові TURBO PASCAL 7.0

Program pmk;

Uses crt;

Var k, p, s, g, x, Integral: real;

n, i, a, b: integer;

BEGIN

writeln ('Введіть проміжок інтегрування (a; b ):');

readln (a);

readln (b);

writeln ('Введіть кількість випадкових значень (число випробувань ):');

readln (n);

k: = ba; {Змінній "k" привласнимо значення довжини проміжку інтегрування}

writeln ('k =', k);

for i: = 1 to n do begin {проведемо n випробувань}

g: = random; {g - мінлива дійсного типу, випадкова величина з проміжку [0; 1]}

x: = a + g * (ba); {За цією формулою виходить довільна величина з [a; b]}

s: = s + (1 + x); {s: = s + (x * x)} {Взагалі можна підставити будь-яку функцію}

delay (1000); {затримка, щоб довільні значення не повторювалися}

end; {кінець випробувань}

writeln ('s =', s); {Сума функції для n довільних значень}

Integral: = (1 / n) * k * s;

writeln ('Інтеграл =', Integral);

readln;

END.

Потрібно вказати проміжок інтегрування і кількість випробувань, інтегрована функція вже задана в програмі (але її можна поміняти).

 ;   . 

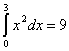Функція	k	N = 10	N = 100	N = 500	N = 1000
f (x) = 1 + x	2	5.737	5.9702	6.02	5.99
f (x) = x * x	3	9.6775	8.528	8.7463	8.937

Висновок

Метод Монте-Карло використовується дуже часто, часом некритично і неефективним чином.

Він має деякі очевидні переваги:

а) Він не вимагає ніяких пропозицій про регулярність, за винятком квадратичної інтегрованості. Це може бути корисним, так як часто дуже складна функція, чиї властивості регулярності важко встановити.

б) Він приводить до здійсненним процедурі навіть у багатовимірному випадку, коли чисельне інтегрування не застосовується.

в) Його легко застосовувати при малих обмеженнях або без попереднього аналізу завдання.

Він має, проте, деякі недоліки, а саме:

а) Межі помилки не визначені точно, але включають якусь випадковість. Це, однак, більш психологічна, ніж реальна, труднощі.

б) Статична похибка зменшується повільно.

в) Необхідність мати випадкові числа.

Література.

1. Гмурман В.Є. Керівництво вирішення задач з теорії ймовірностей та математичної статистики: Навч. посібник для студентів втузів. - 3-е изд., Перераб. І доп. - М.: Вищ. школа, 1979р.

2. Єрмаков С. М. Методи Монте-Карло і суміжні питання. М.: Наука, 1971.

3. Севастьянов Б. А. Курс теорії ймовірностей і математичної статистики. - М.: Наука, 1982.

4. Математика. Великий енциклопедичний словник / Гол. ред. Ю. В. Прохоров. - М.: Велика Російська енциклопедія, 1999р.

5. Гмурман В. Є. Теорія ймовірностей і математична статистика. Учеб. Посібник для втузів. Вид. 5-е, перероб. і доп. М., «Вищ. школа», 1977.