Тема 2.4 Сложный теплообмен

Вопросы темы.

Теплопередача через одно- и многослойную стенку. Коэффициент теплопередачи и термическое сопротивление теплопередаче. Методы интенсификации теплопередачи. Теплопередача через цилиндрическую стенку. Тепловая изоляция.

Теплопроводность при стационарном режиме и граничных условиях третьего рода (теплопередача)

Передача теплоты от одной подвижной среды (жидкости или газа) к другой через разделяющую их твердую стенку любой формы называется теплопередачей. Примером теплопередачи служит перенос теплоты от дымовых газов к воде через стенки труб парового котла, включающий теплоотдачу от горячих дымовых газов к внешней стенке, теплопроводность в стенке и конвективную теплоотдачу от внутренней поверхности стенки к воде. Особенности протекания процесса на границах стенки при теплопередаче характеризуются граничными условиями третьего рода, которые задаются температурами жидкости с одной и другой стороны стенки, а также соответствующими значениями коэффициентов теплоотдачи.

Плоская стенка. Рассмотрим процесс теплопередачи через одно родную плоскую стенку толщиной δ (рисунок ). Заданы коэффициент теплопроводности стенки λ, температуры окружающей среды t_ж1 и t_ж2, коэффициенты теплоотдачи α₁ и α₂. Необходимо найти тепловой поток от горячей жидкости к холодной и температуры на поверхностях стенки t_с1 и t_с2. Плотность теплового потока от горячей среды к стенке определится уравнением

q = α₁ (t_m1 – t_c1).

При стационарном режиме этот же тепловой поток пройдет путем теплопроводности через твердую стенку и будет передан от второй поверхности стенки к холодной среде за счет теплоотдачи:

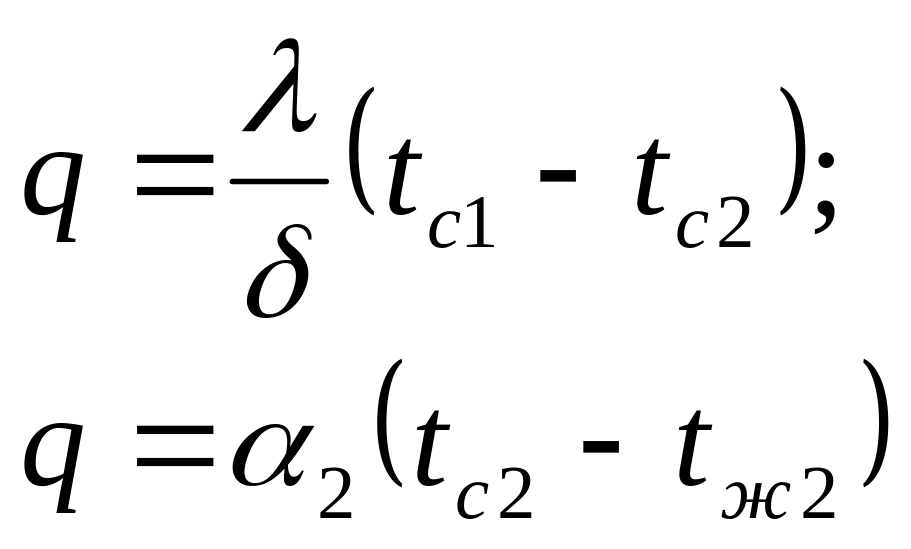
Перепишем уравнения в виде:

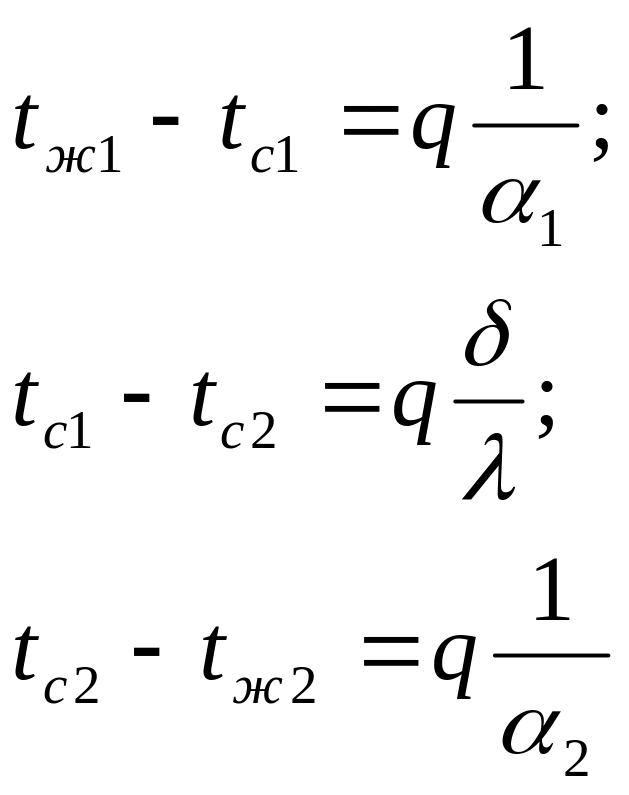
Складывая их почленно, получаем

Отсюда

где

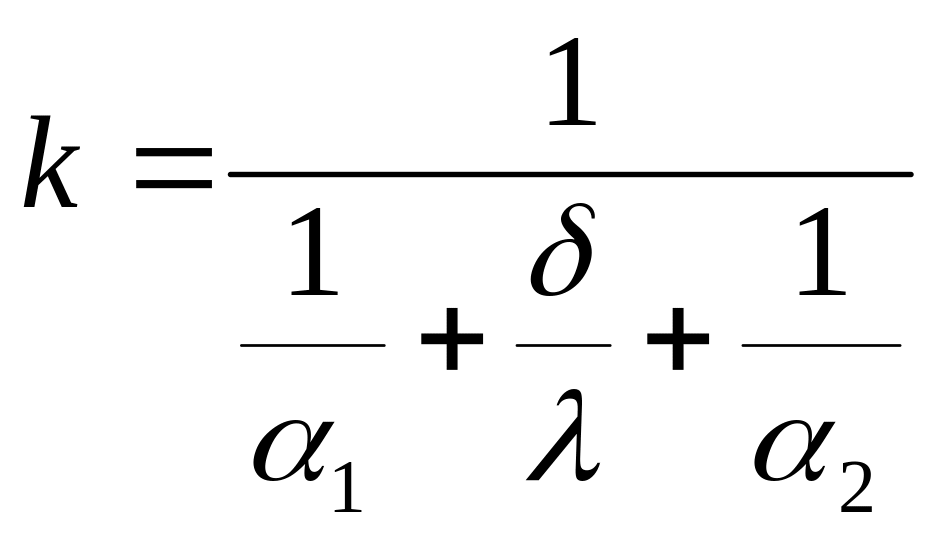
Величина k называется коэффициентом теплопередачи. Численное его значение выражает количество теплоты, проходящее через единицу поверхности стенки в единицу времени при разности температур между горячей и холодной средой в 1 град. Величина, обратная коэффициенту теплопередачи, называется полным термическим сопротивлением теплопередачи

Величины и называется термическими сопротивлениями теплоотдачи. Температуры на поверхностях однородной стенки определяются из уравнений:

В случае многослойной стенки

Отсюда

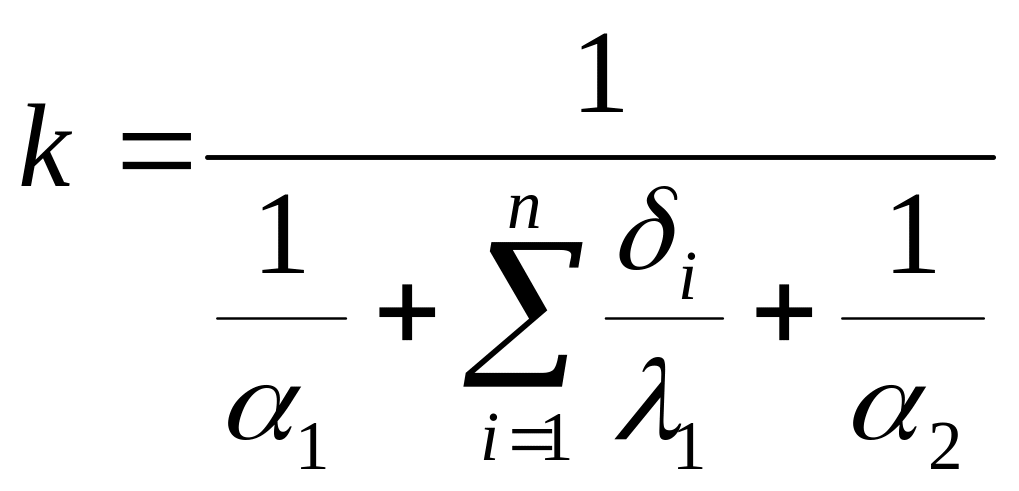
Цилиндрическая стенка. Рассмотрим однородную цилиндрическую стенку с внутренним диаметром d₁, наружным d₂ и постоянным коэффициентом теплопроводности λ (рисунок ). Заданы температуры горячей cреды t_ж1 и холодной t_ж2, соответствующие значения коэффициентов теплоотдачи α₁ и α₂. При установившемся тепловом режиме можно записать:

q₁ = α₁πd₁ (t_ж1 – t_c1 );

Решая полученные уравнения относительно разности температур, а затем складывая, получим

q₁ = k_lπ (t_ж1 – t_ж2 ),

где

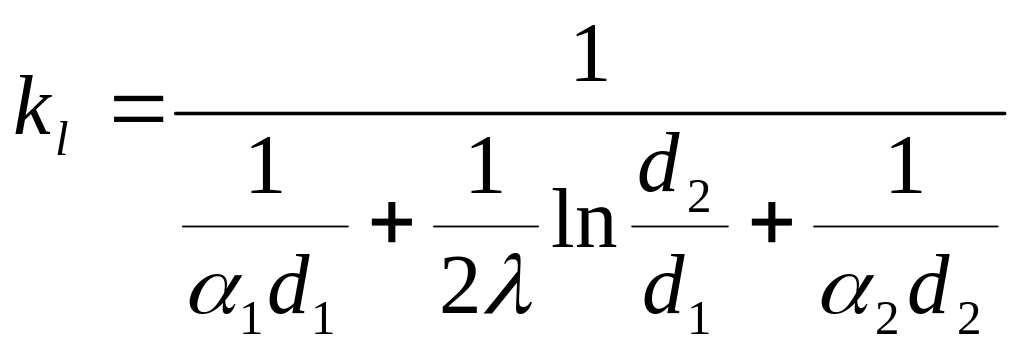
Величина k_l называется линейным коэффициентом теплопередачи и численно равна количеству теплоты, которое проходит через стенку трубы длиной в 1 м за единицу времени при разности температур между горячей и холодной средой 1 град. Величина, обратная линейному коэффициенту теплопередачи, называется полным линейным термическим сопротивлением теплопередачи.

Полное линейное термическое сопротивление теплопередачи складывается из линейных термических сопротивлений теплоотдачи и линейного термического сопротивления теплопроводности В случае многослойной цилиндрической стенки

Тогда

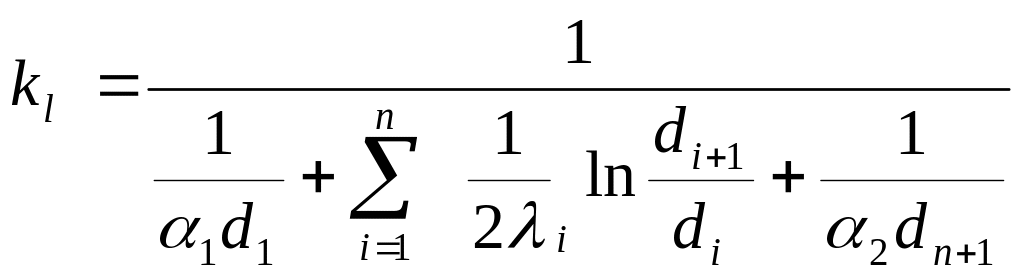
Температуры на поверхностях цилиндрической стенки определяются в результате решения уравнений относительно разности температур:

Критический диаметр изоляции. Тепловой изоляцией называют покрытие из теплоизоляционного материала, которое способствует снижению потерь теплоты в окружающую среду. Рассмотрим случай, когда цилиндрическая стенка покрыта однослойной тепловой изоляцией.

(рисунок ).

Величины α₁, α₂, λ₁, λ_из полагаем заданными. Проследим, как будет изменяться полное линейное термическое сопротивление теплопередачи при изменении толщины изоляции за счет изменения ее диаметра. Воспользовавшись уравнением, запишем

При увеличении внешнего диаметра изоляции d₃ увеличивается R_λиз и одновременно уменьшается R_α2. Возьмем производную от R_l по d₃ и приравняем ее нулю:

Полученное из этого уравнения значение d₃, соответствующее экстремальной точке кривой R_l = f (d₃), называется критическим, т.е.

Вторая производная от R_l в этой точке будет больше нуля. Следовательно, критическому диаметру соответствует минимальное термическое сопротивление и максимальный тепловой поток, определяемый уравнением

q₁ = πk₁ (t_ж1 – t_ж2).

Анализ уравнения показывает, что увеличение диаметра изоляции d₃ в области d₂ < d₃ < d_кр сопровождается ростом тепловых потерь за счет увеличения теплоотдающей поверхности изоляции, при d₃ = d_кр эти потери достигают максимума и только при d₃ > d_кр тепловая изоляция оправдывает свое назначение, т.е. увеличение наружного диаметра изоляции приводит к падению тепловых потерь. Следовательно, для эффективности применения изоляции необходимо, чтобы критический диаметр был меньше внешнего диаметра оголенного трубопровода d₂ или равен ему. В этом случае Подставив в последнее неравенство выражение для d_кр, получаем Отсюда Если это условие не выполнено, то изоляционный материал подобран неправильно.

Интенсификация теплопередачи. Выше были рассмотрены некоторые вопросы выбора теплоизоляционного материала для трубопроводов. Как известно, назначение тепловой изоляции состоит в уменьшении передаваемого через стенку потока теплоты. Наряду с этим в технике приходится решать задачу увеличения плотности теплового потока – интенсификацию теплопередачи. При неизменной разности температур между горячим и холодным теплоносителями передаваемый тепловой поток зависит от коэффициента теплопередачи. Так как теплопередача представляет собой сложное явление, рассмотрение путей ее интенсификации связано с анализом частных составляющих процесса. В случае плоской стенки

Увеличение k может быть достигнуто за счет уменьшения толщины стенки и выбора более теплопроводного материала. Если термическое сопротивление теплопроводности стенки мало, то при

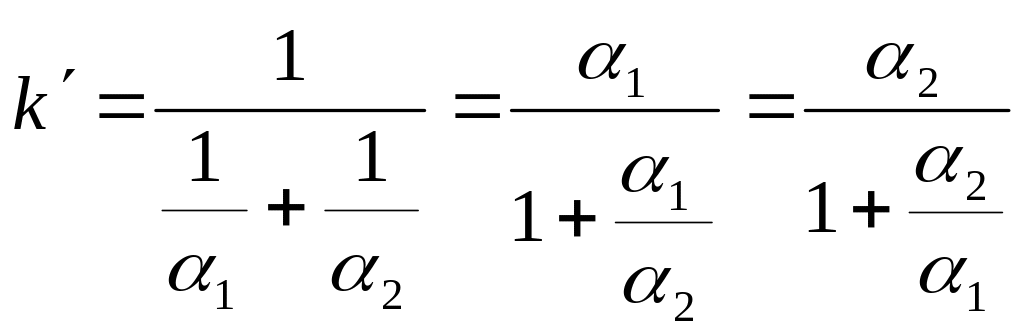
Отсюда видно, что коэффициент теплопередачи всегда меньше самого малого из коэффициентов теплоотдачи. Следовательно, для увеличения коэффициента теплоотдачи нужно увеличивать наименьшее из значений коэффициентов теплоотдачи α₁или α₂. Если α₁ ≈ α₂, то необходимо увеличивать каждый из α.