Ответ 30 Правило Лопиталя

П равило Лопиталя представляет собой метод вычисления пределов, имеющих неопределенность типа или .

Теорема 1 (правило Лопиталя). Пусть две функции определены и дифференцируемы всюду в некоторой окрестности точки , за исключением может быть самой точки . Пусть далее

(1)

и всюду в указанной выше окрестности точки . Тогда, если существует конечное или бесконечное предельное значение , то существует и предельное значение , причем справедлива формула

.

при некоторых условиях предел отношения функций равен пределу отношения их производных

Теорема 2. Пусть две функции определены и дифференцируемы всюду на полупрямой .

Если две функции имеют при бесконечные предельные значения

то отношение двух функций представляет собой при неопределенность вида .

то правило Лопиталя можно применять повторно, то есть предельное значение отношения первых производных функций и можно заменить предельным значением отношения вторых производных. Тогда мы получим

.

Ответ 31 Достаточные условия существования локального экстремума.

Теорема (первое достаточное условие локального экстремума). Пусть точка является точкой возможного экстремума функции , и пусть функция дифференцируема всюду в окрестности точки . Тогда, если в пределах указанной окрестности производная положительна слева от точки и отрицательна справа от точки , то функция имеет в этой точке локальный максимум. Если же производная отрицательна слева от точки и положительна справа от точки , то функция имеет в этой точке локальный минимум. В случае, когда производная имеет один и тот же знак слева и справа от точки , то точка не является точкой локального экстремума.

Теорема (второе достаточное условие локального экстремума). Пусть точка является точкой возможного экстремума функции , и пусть функция имеет в точке конечную вторую производную. Тогда точка является точкой локального максимума, если , и минимума, если .

Ответ 32 Отыскание точек локального экстремума

Точки, в которых функция не является дифференцируемой, могут быть точками локальных экстремумов.

Теорема. Пусть функция дифференцируема всюду в некоторой окрестности точки , за исключением, быть может, самой точки , и непрерывна в точке . Тогда, если в пределах указанной окрестности производная положительна (отрицательна) слева от точки и отрицательна (положительна) справа от точки , то функция имеет в этой точке локальный максимум (минимум).

Пример. Найти точки экстремума функции .

Данная функция непрерывна на всей числовой оси. Е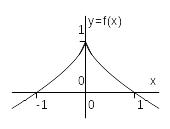 е производная определена всюду на этой прямой за исключением точки . Поскольку при , а при , то точка является точкой локального максимума. Функция принимает в этой точке наибольшее значение, равное 1. Так как , то график функции касается оси в точке .

Дополнительный вопрос Условия монотонности функции на интервале

Теорема. Для того, чтобы дифференцируемая на интервале функция не убывала (не возрастала) на этом интервале необходимо и достаточно, чтобы производная этой функции была неотрицательной (неположительной) на этом интервале.

Если всюду на интервале производная функции положительная (отрицательная), то функция на этом интервале строго возрастает (строго убывает).

Необходимость. Пусть функция не убывает на интервале . Рассмотрим произвольную точку , принадлежащую данному интервалу, и выберем достаточно малое положительное приращение аргумента такое что . Тогда . Следовательно,

.

Переходя в последнем неравенстве к пределу при , получим

.

Достаточность. Пусть для любого . Пусть . Функция является дифференцируемой и, следовательно, непрерывной на отрезке . Тогда по формуле Лагранжа имеем , где . Так как и , то . Следовательно, функция не убывает.

Если же , то , то есть функция строго возрастает.