Ответ 25

таблица производных основных элементарных функций. Вывод формул.

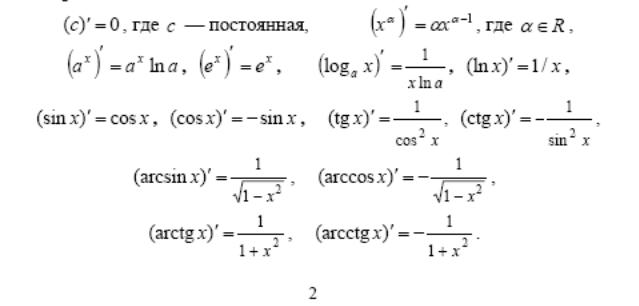
Вывод формул для вычисления производных некоторых элементарных функций.

1. , где — некоторая постоянная.

Для данной функции и .

2. .

,

.

3. .

,

.

4. .

,

.

Из последней формулы следует, что

.

5. .

,

.

В частном случае, при , имеем

.

6. , где — натуральное число.

Воспользовавшись формулой бинома Ньютона получим

,

.

Ответ 26 Производные высших порядков

Пусть функция определена и дифференцируема на интервале . Тогда ее производная представляет собой функцию переменной также определенную на интервале . в свою очередь может оказаться дифференцируемой в некоторой точке интервала . Производную от функции называют второй производной (производной второго порядка) от функции и обозначают или . Итак,

.

Далее мы можем аналогично ввести понятие третьей производной, как производной от второй:

,

затем четвертой и т. д.

Соотношение, определяющее -ю производную имеет вид

.

Определение. Функция, имеющая на данном множестве , конечную производную порядка называется раз дифференцируемой на данном множестве.

Ответ 27

Теоремы о непрерывных функциях.

Теорема. Пусть заданные на одном и том же множестве функции и непрерывны в точке . Тогда функции , , и также непрерывны в точке (частное при условии ).

Теорема. Если функция непрерывна в точке , а функция непрерывна в точке , соответствующей точке , то функция непрерывна в точке .

Ответ 28

Локальный максимум и локальный минимум функции в точке. Локальные экстремумы. Необходимое условие локального экстремума дифференцируемой функции (теорема Ферма)

Определение. Точка называется точкой локального максимума, если найдется -окрестность точки , в пределах которой значение является наибольшим, то есть для любого из интервала справедливо неравенство .

Определение. Точка называется точкой локального минимума, если найдется -окрестность точки , в пределах которой значение является наименьшим, то есть для любого из интервала справедливо неравенство .

Если — точка локального минимума или максимума, то говорят, что функция имеет в этой точке локальный минимум или локальный максимум.

Локальный максимум и локальный минимум объединяются общим названием локальный экстремум.

Теорема Ферма (необходимое условие локального экстремума дифференцируемой функции). Если функция дифференцируема в точке и имеет в этой точке локальный экстремум, то .

Ответ 29 Теорема Ролля. Теорема Лагранжа. Теорема Коши

Теорема Ролля. Пусть функция непрерывна на отрезке и дифференцируема во всех внутренних точках этого отрезка. Пусть, кроме того, . Тогда внутри отрезка найдется точка такая, что значение производной в этой точке равно нулю.

Теорема Лагранжа. Если функция непрерывна на отрезке и дифференцируема во всех его внутренних точках, то существует, по крайней мере, одна точка , в которой .

Теорема Коши. Если функции и непрерывны на отрезке и дифференцируемы во всех его внутренних точках, причем не обращается в ноль ни в одной из указанных точек, то существует, по крайней мере, одна точка , в которой .