Ответ 9. Бесконечно малые и бесконечно большие функции. Сравнение бесконечно малых и бесконечно больших функций
Определение.
Функция
называется бесконечно малой
в точке
(при
),
если ее предельное значение в этой точке
(при
)
равно нулю.
Определение
(по Гейне). Функция
называется бесконечно большой в
точке
справа (слева), если
для любой сходящейся к
последовательности
значений аргумента
,
все элементы которой больше (меньше)
,
соответствующая последовательность
значений функции
является бесконечно большой
последовательностью определенного
знака.
Если
Функция
является бесконечно большой в точке
справа (слева), то ее предел считают
равным
или
.
Определение (по Гейне). Функция называется бесконечно большой при ( ), если для любой бесконечно большой последовательности значений аргумента , все элементы которой положительны (отрицательны), соответствующая последовательность значений функции является бесконечно большой последовательностью определенного знака.
Функция
называется бесконечно малой более
высокого порядка, чем
,
если
.
В этом случае используют символическую
запись
,
которая читается следующим образом:
равно
малое от
.Функции и называется бесконечно малыми одного порядка, если в точке существует конечный предел отношения
,
отличный от нуля.Функции и называется эквивалентными бесконечно малыми, если
.
Для обозначения эквивалентности
используют символ ~. Запись
читается: функция
эквивалентна
функции
.Функция называется бесконечно малой порядка
относительно
,
если в точке
существует конечный предел отношения
,
отличный от нуля.
Аналогичным
образом сравнивают и бесконечно большие
функции. Пусть
и
— две бесконечно большие в точке
справа (либо слева) функции одного знака.
Ответ 10.
Предельное значение арифметические значения алгебраического многочлена и рациональной функции
Предельное значение
алгебраического многочлена
в точке
равно значению многочлена в этой точке.
Предельное
значение рациональной функции переменной
в
точке
равно частному
значению рациональной функции в этой
точке, где
и
— алгебраические многочлены степени
и
соответственно, равно частному значению
рациональной функции в этой точке.
.
Ответ 11.
Неравенство
.
Предельные значения тригонометрических
функций.
Докажем, что при
справедливо неравенство
. (1)
П
усть
.
Рассмотрим окружность единичного
радиуса с центром в точке
(рис. 1). Пусть радиус
образует угол
с радиусом
.
Соединим точки
и
отрезком прямой и восстановим из точки
перпендикуляр к радиусу
до пересечения с продолжением
.
Точку пересечения обозначим
.
Тогда
и
.
Найдем площади треугольника
,
сектора
и треугольника
:
,
,
.
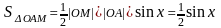Поскольку треугольник содержится в секторе , который в свою очередь содержится в треугольнике , то их площади связаны соотношением
.
Следовательно,
,
откуда
(
).
Если
,
то
и будет выполняться неравенство
.
Отсюда, учитывая нечетность функций
и
,
получим
(
)
Если
,
то
.
Итак, мы доказали, что для любого
из интервала
справедливо неравенство (1).
Предельные значения тригонометрических функций:
функции и
не имеют предельного значения при
.
,
при
(
)на интервале
,
на интервале
.
,
при
(
)
Ответ 12
Первый замечательный предел и его свойства
Теорема.
Предельное значение функции
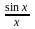в точке
существует и равно единице:
.
(1)
Равенство (1) называют первым замечательным пределом.
Следствие.
;
;
Ответ 13
Второй замечательный предел и его свойства
Теорема.
Предельное
значение функции
при
существует и равно
:
.
(1)
Второй замечательный предел также записывают в виде
.
(2)
Следствие:.
;
;
Ответ 14
Понятие непрерывности функции в точке. Непрерывность функции на множестве. Точки разрыва. Классификация точек разрыва
Определение.
Функция
называется непрерывной в точке
,
если предельное значение этой функции
в точке
существует и равно частному значению
,
то есть, если
.
(1)
Определение. Функция называется непрерывной справа (слева) в точке , если правое (левое) предельное значение этой функции в точке существует и равно частному значению .
,
Определение. Функция называется непрерывной на множестве , если она непрерывна в каждой точке этого множества.
Определение. Точки, в которых функция не является непрерывной, называются точками разрыва функции.
Классификация точек разрыва
Устранимый разрыв. Точка называется точкой устранимого разрыва функции , если предельное значение функции в этой точке существует, но либо функция не определена в этой точке, либо ее предельное значение не равно частному значению .
Если функция имеет в точке разрыв такого рода, то его можно устранить, определив значение функции в точке равным ее предельному значению в этой точке.
Разрыв первого рода. Точка называется точкой разрыва первого рода, если в этой точке функция имеет конечные, но не равные друг другу правое и левое предельные значения:
.
Разрыв второго рода. Точка называется точкой разрыва второго рода, если в этой точке функция не имеет хотя бы одного одностороннего предельного значения, или если, по крайней мере, одно из односторонних предельных значений бесконечно.
Определение. Функция называется кусочно непрерывной на отрезке , если она непрерывна во всех внутренних точках этого отрезка, за исключением, может быть, конечного числа точек, в которых имеет разрыв первого рода, и, кроме того, имеет односторонние предельные значения в точках и .
Ответ 15
Арифметические операции над непрерывными функциями в точке.
Теорема.
Пусть заданные на одном и том же множестве
функции
и
непрерывны в точке
.
Тогда функции
,
,
и
также непрерывны в точке
(частное при условии
).
Поскольку
и
непрерывны в точке
,
то
и
.
Используя теорему об арифметических
операциях над функциями, имеющими
конечные предельные значения, получим:
,
,
.
Ответ 16
Сложная функция и ее непрерывность
Функции, образованные в результате суперпозиции двух или нескольких функций - сложные функции.
Пусть
функция
определена на некотором множестве
,
а
— множество значений этой функции. Если
на указанном множестве
определена другая функция
,
то говорят, что на множестве
задана сложная функция переменной
.
Теорема.
Если функция
непрерывна в точке
,
а функция
непрерывна в точке
,
соответствующей точке
,
то функция
непрерывна в точке
.