ТиОтветы на билеты по мат. Анализу. Ответ 1. Понятие множества и отображения. Подмножества. Равные множества. Операции над множествами.

Под множеством понимается совокупность элементов (объектов) той или иной природы.

Множества обычно обозначают большими буквами латинского или другого алфавита: …, а элементы множества малыми буквами …

Если элемент принадлежит множеству , то пишут . Если не принадлежит множеству , то запись этого утверждения имеет вид .

Существует два основных способа задания множества.

1.Если элементы множества могут быть перечислены, то такое множество записывают в виде . Множество , где — целое положительное число, состоит из бесконечного числа элементов. Если множество состоит из элементов , где индекс принимает значения из некоторого множества , то его записывают в виде .

2.Если множество состоит из элементов, обладающих определенным свойством, то его записывают в виде , где в фигурных скобках после вертикальной черты указывают данное свойства элементов множества. Например, если множество — это отрезок ( ), то есть множество всех чисел , удовлетворяющих неравенству , то форма записи множества имеет вид .

Отображения. Закон F, согласно которому каждому элементу поставлен в соответствие единственный элемент , называется отображением множества X в множество Y или функцией, заданной на X со значениями в Y.

Y

X

x

y

f^--1

f

Равные множества. Множества и называются равными, если они состоят из одних и тех же элементов , то есть равенство означает, что одно и тоже множество обозначено разными буквами.

Подмножества. Множество называется подмножеством множества , если каждый элемент множества принадлежит множеству . В этом случае пишут . Последнюю запись можно прочитать и так: множество заключено (содержится) в множестве .

О бъединением или суммой множеств и называется множество , состоящее из всех элементов, принадлежащих хотя бы одному из множеств и . Объединение множеств и обозначается символом .

П ересечением множеств и называется множество , состоящее из всех элементов, принадлежащих как множеству , так и множеству , Пересечение множеств и обозначается через .

Р азностью множеств и называется множество , состоящее из элементов, принадлежащих множеству , но не принадлежащих множеству , то есть .

Е сли , то разность называется дополнением множества до множества и обозначается .

Ответ 2. Действительные числа и их представление в виде бесконечных десятичных дробей. Числовые множества. Ограниченные и неограниченные множества

натуральный ряд чисел это Множество этих чисел называется множеством натуральных чисел и обозначается . В результате вычитания или деления не всегда получаются натуральные числа, и возникает необходимость расширить класс рассматриваемых чисел.

Вводятся число 0 и отрицательные числа –1, -2, …,-n, … Натуральные числа, число 0 и указанные отрицательные числа образуют множество целых чисел . Очевидно, что множество натуральных чисел является подмножеством целых чисел, то есть .

При делении целых чисел появляются рациональные числа вида , где и — целые числа, причем . Множество рациональных чисел обозначают буквой . Его можно записать в виде . рациональное число — это несократимая обыкновенная дробь.

извлечение корня, вычисление логарифмов, значений тригонометрических функций и прочие операции привели к появлению иррациональных чисел. Все рациональные и иррациональные числа образуют множество вещественных (действительных) чисел. Множество вещественных чисел обозначают 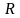. Очевидно, справедливо соотношение .

Рассмотрим алгоритм измерения длины произвольного отрезка . Ради определенности предположим, что точка лежит по ту же сторону от точки , что и точка . Используем для измерения длины отрезка масштабный отрезок , считая его длину равной 1.

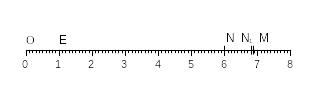
Рис. 4

Отрезок либо укладывается в отрезке раз с некоторым остатком , меньшим , либо отрезок уложится в отрезке ровно раз без остатка (рис. 4). Тогда целое число представляет собой приближенный результат измерения по недостатку с точностью до единицы: = Причем во втором случае остаток равен . Заметим также, что длину мы считаем равной единице.

Далее выясним сколько раз часть отрезка укладывается в остатке . Если часть отрезка укладывается в отрезке раз с остатком , не большим части отрезка , то — это длина отрезка , измеренного по недостатку с точностью до , а следовательно представляет результат измерения длины отрезка по недостатку с точностью до 0,1. Здесь — целое неотрицательное число. Заметим также, что поскольку длина отрезка не превышает единицы, то не может быть больше 9.

Если часть отрезка укладывается в отрезке раз ( ) с остатком , не большим части отрезка , то число представляет результат измерения длины отрезка по недостатку с точностью до 0,01.

Продолжая неограниченно процесс измерения по указанному алгоритму, получим бесконечную десятичную дробь , которая задает длину отрезка и может быть поставлена в соответствие точке .

Указанные рассуждения можно применить и к точке, лежащей левее точки . Только в этом случае бесконечная десятичная дробь будет отрицательной.

Итак, мы установили, что любой точке числовой оси может быть поставлена в соответствие бесконечная десятичная дробь вида , где , , , . Дробь берут со знаком «плюс», если точка расположена правее начала отсчета и со знаком «минус» в противном случае.

Ограниченные и неограниченные множества.

Определение. Множество вещественных чисел называется ограниченным сверху (снизу), если найдется такое вещественное число , что для каждого элемента множества справедливо неравенство ( ). При этом число называют верхней гранью множества , а число — нижней гранью множества .

Любое ограниченное сверху (снизу) множество имеет бесконечное число верхних (нижних) граней. Действительно, если , то . Следовательно, также является верхней гранью.

Определение. Множество вещественных чисел называется неограниченным сверху (снизу), если для любого вещественного числа найдется элемент множества , удовлетворяющий неравенству ( ).

Определение. Число ( ) называется максимальным (минимальным) элементом множества , если для всех элементов данного множества справедливо неравенство ( ) и ( ) принадлежит множеству .

Определение. Множество называется ограниченным, если оно ограничено сверху и снизу, то есть найдутся два вещественных числа и такие, что для любого элемента множества справедливо неравенство .

Определение. Множество называется неограниченным, если для любого положительного числа найдется элемент множества , удовлетворяющий неравенству .