32. Достаточное условие локального экстремума функции n переменных.

Пусть функция u=f(X1, X2, …, Xn) 1 раз дифференцируема в окрестности точки

Мо( и 2 раза дифференцируема в самой точке Мо. Кроме того Мо – стационарная точка. Тогда

1. если d²u положительно определенная квадратичная форма от переменных dx1, dx2,…, dxn, то функция имеет в точке Мо локальный min

2. если d²u отрицательно определенная квадратичная форма от переменных dx1, dx2,…, dxn, то функция имеет в точке Мо локальный max

3. если d²u знакопеременная квадратичная форма от переменных dx1, dx2,…, dxn, то экстремума в точке Мо не существует.

Следствие: Пусть функция 2 переменных u=f(x, y) 1 раз дифференцируема в окрестности точки Мо и 2 раза дифференцируема в точке Мо и Мо – стационарная точка. Тогда если в точке Мо выполняется условие Ai=a11*a22 – a12*a21>0, то экстремум существует; если a11>0, то Мо – min; если a11<0, то Mo – max. Если a11*a22 – a12*a21<0, то экстремума не существует.

33. Неявные функции.

ОПР: если переменная u является по смыслу функцией аргументов X1, X2, …, Xn, задается по средством функционального уравнения F(u, X1, X2,…, Xn)=0, то она задана неявно.

Частные производные неявной функции вычисляются по формулам:

,…,

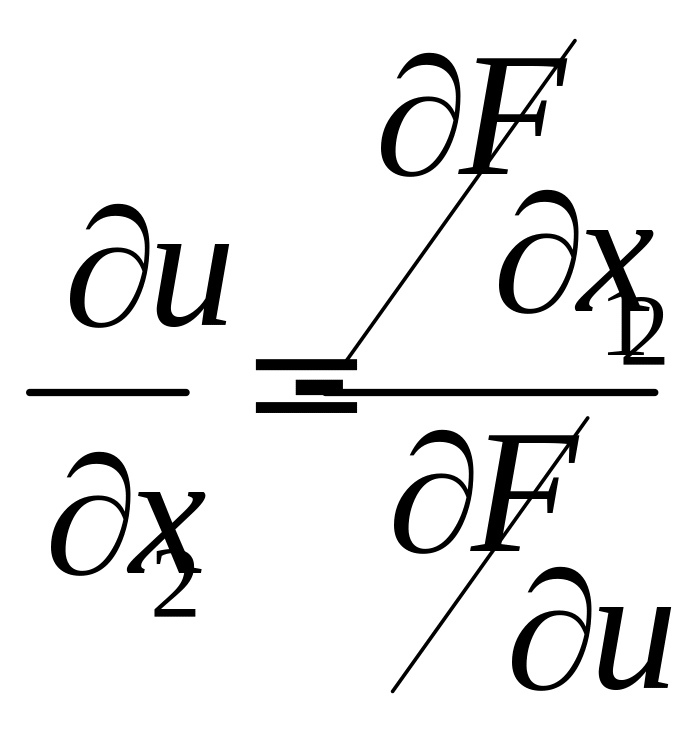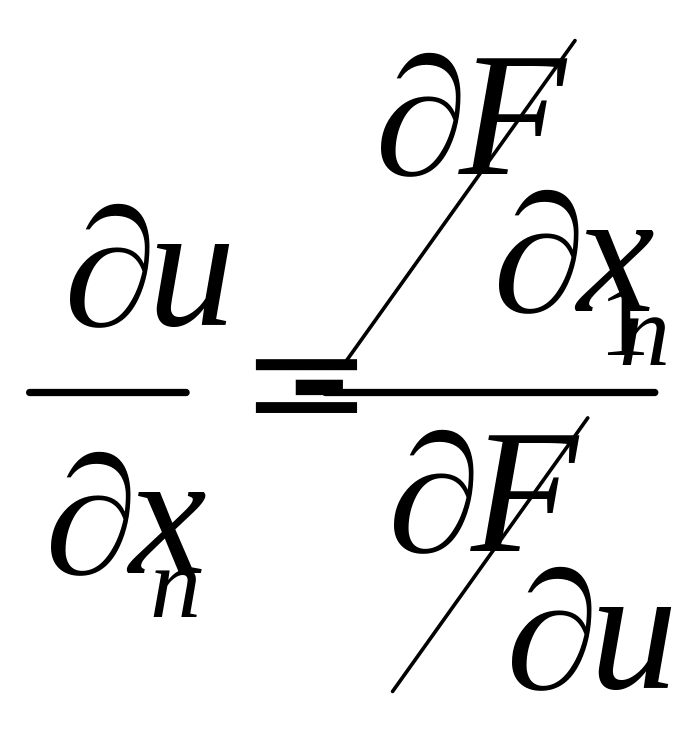
Рассмотрим совокупность m неявных функций, которые задаются посредством системы m функциональных уравнений:

F1(u1, u2,…, um, x1, x2,…, xn)=0

F2(u1, u2,…, um, x1, x2,…, xn)=0 (1)

----------------------------------------

Fm(u1, u2,…, um, x1, x2,…, xn)=0

Пусть u1, u2,…,um функции переменных x1, x2,…,xn определены как решение системы m функциональных уравнений (1).

U1=1(x1, x2,…, xn)

U2=2(x1, x2,…, xn) (2)

-----------------------

U3=3(x1, x2,…, xn)

Поставим вопрос о разрешимости системы (1) относительно u1, u2,…,um

ОПР: под решением системы (1) понимать совокупность m функций таких, что при подстановке их в систему (1) все уравнения системы обращаются в тождества.

ОПР: это решение непрерывно и дифференцируемо в области D (изменение переменных x1, x2,…,xn), если каждая из функций u1, u2,…,um непрерывна и дифференцируема в этой области.

Введем в рассмотрение определитель Якобиана.

ТЕОР: система (1) будет разрешима, а решение непрерывно и дифференцируемо, если Якобиан не равен 0.

34. Условный экстремум.

ОПР: задача отыскания экстремума функции, аргументы которой удовлетворяют дополнительному условию связи называется задачей нахождения условного экстремума.

Рассмотрим вопрос отыскания условного экстремума функции

F1(u1, u2,…, um, x1, x2,…, xn)=0

F2(u1, u2,…, um, x1, x2,…, xn)=0 (1)

----------------------------------------

Fm(u1, u2,…, um, x1, x2,…, xn)=0

ОПР: (3) Z=f(u1, u2,…, um, x1, x2,…xn)extr при наличии условных связей (1). Будем говорить, что функция (3) при наличии условной связи (1) имеет условный max в точке Мо, координаты которой удовлетворяют условной связи (1). Если существует окрестность точки Мо, в пределах которой значение функции Z в Мо является наибольшим среди ее значений во всех точках, координаты которых удовлетворяют условию связи (1). Аналогично вводится понятие min.

Iспособ: пусть функции F1, F2,…,Fm дифференцируемы в окрестности точки Мо, частные производные непрерывны в окрестности этой точки и Якобиан

не равен 0. Тогда система (1) имеет непрерывное, дифференцируемое решение в функции (3), получаем задачу определения безусловного экстремума.

(4) Z=f(1(x1, x2,…, xn), 2(x1, x2,…, xn),…, m(x1, x2,…, xn), x1, x2,…xn)extr

II способ: Если система (1) неразрешима или определить ее решение затруднительно, то используется более универсальный метод решения задач условного экстремума – метод множителей Лагранжа.