28. Частные производные высших порядков функции n переменных.

Рассмотрим функцию u=f(x,y,z) вычислим частную производную

Пусть все частные производные существуют в каждой точке множества {M}=D(f) Поставим вопрос о нахождении частных производных по всем переменным по функции :

ОПР: Частная производная взятая от по переменной Хк называется частной производной второго порядка и обозначается , если I=k, то она обозначается как

Смешанные частные производные второго порядка для непрерывной функции равны.

Аналогично, равные смешанные частные производные 3, 4 и т.д.

29. Дифференциал второго порядка функции n переменных.

Определение дифференциала

u=f(x1,x2,…,xn), y=f(x), dy=f’(x)dx, d²y=(dy)

ОПР: Значение дифференциала  взятого от дифференциала первого порядка du в предположении, что х1=dx1…xn=dxn. Называется вторым дифференциалом функции в данной точке М(x1,x2,…xn), а вычисляется по формуле

D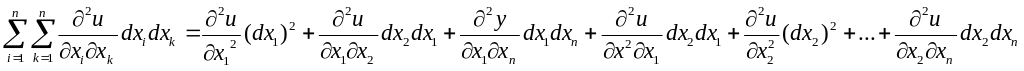 ²u=

+…+

30. Квадратичная форма. Критерий сильвестра.

Рассмотрим функцию специального вида. Квадратичная форма:

ОПР: Функция Ф(t1,t2,…,tk)= называется квадратичной формой, где Аik коэффициенты квадратичной формы, - переменные квадратичные формы, d²u квадратичная форма относительно dx1, ….,dxn c коэффициентом Aik= . Если Aik=Aki, то квадратичная форма называется симметричной. Данной квадратичной форме ставится в соответствие матрица коэффициентов квадратичной формы.

ОПР: Матрицей А размера mn называется прямоугольная таблица чисел содержащая m строк и n столбцов.

ОПР: Матрица называется квадратной, если число строк равно числу столбцов.

ОПР: Симметричной: Aik=Aki

ОПР: Определителем матрицы называется число характеризующее матрицу detA

Существуют способы вычисления det:

ОПР: Минор - некоторый фрагмент матрицы.

ОПР: Главными минорами матрицы А называются следующие определители:

А1=А11

А2=а11*А22-А21*А12

А3=А11*А22*А 33+А21*А22*А13+А31*А22*А13 – А32*А23*А11 – А21*А12*А33

Аm=det A

ОПР: Квадратичная форма называется положительно определенной, если для любых значений t1,t2,…, tn одновременно не равных 0 она принимает строго положительные значения.

ОПР: Квадратичная форма называется отрицательно определенной если для любых значений неравенств t1,t2,…tn она принимает строго отрицательные значения.

ОПР: Квадратичная форма называется знакопеременной, если она принимает как строго положительные, так и строго отрицательные значения при различных наборах t1,t2,…tn

Критерий Сильвестра знакопеременной квадратичной формы:

1. Для того, чтобы квадратичная форма или матрица была положительно определенной необходимо и достаточно, чтобы все главные миноры матрицы А были положительными.

2. Для того чтобы квадратичная форма или матрица была отрицательно определенной необходимо и достаточно, чтобы знаки главных миноров чередовались, причем первый был отрицательный.

Замечание: если хоть одно из условий не выполняется, то форма знакопеременная.

31. Локальный экстремум функции n переменных. Необходимое условие локального экстремума.

ОПР: будем говорить, что функция u=f(M) имеет локальный max (min) в точке Мо, если существует такая -окрестность точки Мо, в пределах которой значение функции f(Mo) является наибольшим (наименьшим) по сравнению со значениями f(M) в любой точке М из этой окрестности.

ТЕОР: Необходимое условие: Если функция u=f(M) обладает в точке М частной производной I порядка по всем переменным и имеет в этой точке локальный экстремум. То все частные производные I порядка в этой точке обращаются в 0.

Все точки, в которых выполняется это условие, называются стационарными.