2.4. Интегральная теорема Лапласа

Мы видели, что отыскание вероятности появления события А при п испытаниях, количество которых заключено в границах целых чисел а и b, было связано с применением теоремы сложения вероятностей. Именно, если т принимает значения всех последовательных целых чисел , где и то вероятность того, что событие А наступит либо раз, либо раз, ..., либо раз, т. е. вероятность появления события А при п испытаниях не менее а и не более b раз, определяется по формуле

Отыскание этой суммы с помощью данных биномиального распределения по мере возрастания числа п сопровождается значительными затруднениями вычислительного характера. Между тем такая задача может быть успешно разрешена приближенно и притом с желательной степенью точности на основании интегральной теоремы Лапласа.

Теорема. Если производится большое число п независимых испытаний, в каждом из которых вероятность наступления события А равна р, то вероятность того, что число т появлений события А удовлетворяет неравенству

имеет своим пределом

когда п неограниченно возрастает.

Математическая запись этой теоремы:

Доказательство. Пусть число п независимых испытаний зафиксировано. Тогда принятые в условии границы значений m — определенные целые числа.

Обозначив их через а и b, будем иметь:

и ¹⁾.

Искомая вероятность в указанных границах числа т определяется согласно теореме сложения вероятностей

При этом значения слагаемых вычисляются либо (для небольших п и т) по формуле Бернулли, либо по формуле Лапласа.

Отыскание же предела, к которому стремится вероятность

при неограниченном возрастании числа п, может быть осуществлено только с помощью определенного интеграла.

Приведем поэтому выражение к виду интегральной суммы.

Общий член суммирования

мы можем представить, пользуясь асимптотической формулой биномиального распределения, в виде

Здесь при для всех целых т в заданных границах. Но переход к переменной х связан с выделением в общем члене суммирования множителя и с установлением границ для переменной х.

При рассмотрении асимптотической формулы было принято соотношение

(1)

Это соотношение приводит в соответствие числу значение , числу - значение и т. д.

Так как паре последовательных чисел m и т +1 соответствует пара значений x и , то имеем два соотношения:

и

Отсюда вычитанием находим

а это показывает, что условие непосредственно влечет за собой условие

Таким образом, общий член интегральной суммы может быть записан в виде

(здесь вместе с ).

Границы значений переменной х определяются из условия теоремы о границах числа т. В самом деле, переписав соотношение (1) в виде

можно на основании неравенств

установить, что значения х заключены в границах чисел  и , т.е.

При фиксированном п имеем интегральную сумму

которая с изменением п является переменной величиной.

Переход к пределу (для левой части при , а для правой части при ) обращает в нуль второе слагаемое в правой части, и отсюда

Полученное равенство можно переписать в соответствии с формулировкой рассмотренной теоремы:

Дадим геометрическое истолкование теоремы. Чтобы графически представить преобразованный общий член интегральной суммы , обратимся к кривой, соответствующей функции (рис. 4).

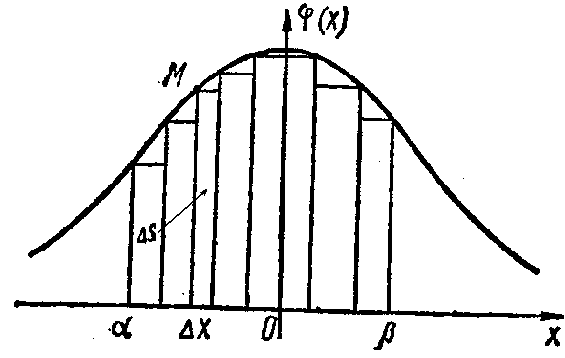
Рис. 4

Если М — произвольная точка на этой кривой, то произведению будет соответствовать площадь прямоугольника с высотой, равной ординате точки М [это — значение функции ], и с основанием, равным элементарному отрезку на оси Ох, соответствующему в силу соотношения (1) приращению на 1 числа m появлений события А.

Интегральная сумма, выражающая приближенное значение искомой вероятности, численно равна площади ступенчатой фигуры, составленной из элементарных прямоугольников в заданных границах между  и .

Полученный определенный интеграл, дающий предельное значение той же вероятности при , численно равен площади криволинейной трапеции, ограниченной сверху кривой

,

снизу осью Ох и с боков перпендикулярами к оси Ох в точках и .

До перехода к применению полученного результата при вычислении вероятностей рассмотрим частный случай, когда число т принимает все возможные значения от 0 до п, т.е. когда ищется

Так как условие связано с достоверностью события, то

и это сохраняется при неограниченном возрастании числа независимых испытаний, т. е. и

Найдем пределы соответствующего этому случаю интеграла, т. е. границы значений переменной х.

Из соотношения (1) можно установить, что при а из следует ; при а из следует .

Отсюда

и, таким образом,

Из установленной сходимости этого интеграла (его называют интегралом Лапласа) непосредственно следует, что

а отсюда легко перейти и к интегралу Пуассона.

Действительно, замена дает

и

Поэтому

Интегральная теорема Лапласа применяется для вычисления вероятности того, что число т появлений события А заключено в фиксированных границах

при заданном числе испытаний. Поэтому соответствующая формула приобретает уже приближенный характер, т. е.

и точность достигаемого результата повышается с возрастанием количества испытаний.

Самое отыскание вероятностей связано с определением численных значений найденного интеграла Лапласа

При этом для непосредственных вычислений принята специальная функция, представляющая удвоенный интеграл Лапласа, т. е. Функция

значения которой находятся, например, с помощью степенных рядов.

Эта функция имеет следующие два свойства:

1) с возрастанием х значения Ф(х) возрастают, приближаясь к единице;

2) так как ряд, представляющий эту функцию, состоит из нечетных степеней х, то , т. е. эта функция нечетная. Численные значения функции Ф(х) даются в специальной таблице, и это позволяет находить интеграл

по следующей формуле:

Справедливость этой формулы может быть установлена учащимся.

Таким образом, вся операция состоит в отыскании значений  и , соответствующих границам а и b, с последующим обращением к табличным значениям и , и в использовании формулы

Пример 13. Вероятность попадания в цель из скорострельного орудия равна при отдельном выстреле 0,8. Найти вероятность того, что число попаданий при 900 выстрелах будет заключено в границах чисел 690 и 740.

Решение. Здесь n = 900,

Соотношения

и

здесь дают:

и

Отсюда

Искомая вероятность

Пример 14. При вытачивании болтов наблюдается в среднем 10% брака. Можно ли быть уверенным, что в партии из 400 болтов окажутся пригодными более 299?

Решение. Принимая р = 0,9, будем искать .

Значения  и  определим из соотношений:

и

Отсюда

и

Таким образом,

Но оба значения Ф(х) выходят из границ таблицы, которая составлена для значений х не свыше 4,50. Значениям же х > 4,50 соответствуют значения Ф(х), мало отличающиеся от 1, и поэтому искомая вероятность практически принимается равной 1.

Это означает, что наличие в данной партии более 299 пригодных болтов можно считать достоверным.

Следует заметить, что формула для вычисления вероятности по теореме Лапласа несколько упрощается в случаях, когда границы а и b для возможного числа появлений события А симметричны относительно числа пр, т. е.

и

Тогда

Пример 15. Пусть при , р=0,8 и q=0,2 требуется найти

Решение. Здесь и поэтому значение  можно найти из соотношения где и .

Значит , а отсюда

Использование функции Ф(х) позволяет также ответить на вопрос о вероятности того, что отклонение частости события ( ) от его вероятности в отдельном испытании (p) не превысит заданной величины. Такой результат достигается следующим преобразованием неравенств (в теореме Лапласа).

Деление всех членов неравенств на п дает:

Эти неравенства эквивалентны неравенствам:

Если абсолютная величина отклонения то , и тогда в силу сохранения вероятности выполнения эквивалентных неравенств имеет место соотношение

или

Переход к заданной величине отклонения  дает

Этот результат позволяет с помощью функции Ф(х) установить вероятность того, что отклонение частости события при п испытаниях от его вероятности по абсолютной величине не превышая заданного числа .

Пример 16. Вероятность появления события А в отдельном испытании р=0,6. Найти вероятность того, что при 150 испытаниях частость появления этого события будет отличаться от его вероятности не более чем на 0,03.

Решение. Здесь надо искать при условиях , , и Так как

то