5.2. Критерий Уилкоксона

Область применения. Критерий Уилкоксона применяется в той же ситуации, что и критерий Манна-Уитни. В отличие от этого критерия и критерия знаков, он имеет дело не со знаками некоторых случайных величин, а с их рангами. Исторически критерий Уилкоксона был одним из первых критериев, основанных на рангах (о рангах см. п. 3).

Рассмотрим ранги элементов объединения двух выборок и . Для получения рангов совокупность всех наблюдений следует упорядочить в порядке возрастания. (Напомним, что если функции распределения F и G выборок х и у непрерывны, то в их совокупности нет совпадающих значений и, следовательно, результат упорядочивания однозначен. Как поступать в противном случае, будет сказано ниже, в разделе «совпадения».

Пусть, например, первая выборка состоит из чисел 6, 17 и 14, вторая — из чисел 5 и 12. Тогда ранги величин первой группы есть 2, 5, 4, второй — 1, 3.

Нетрудно понять, что последовательность рангов совокупности oбъема т+n является некоторой перестановкой чисел 1,..., m+n. Верно и обратное: любая перестановка чисел 1,..., m + п может оказаться ранговой последовательностью. Так что множество возможных ранговых последовательностей — это совокупность перестановок чисел 1, 2,..., m+n. Их общее число равно (m+n)!.

Зная распределения случайных величин и , мы можем (по крайней мере, теоретически) вычислить вероятность того, что результат их ранжирования будет заданной перестановкой. Поэтому каждое распределение случайных величин и порождает некоторое распределение вероятностей на указанном множестве перестановок. Ясно, что если исходные данные однородны ( и в совокупности являются независимыми и одинаково распределенными случайными величинами), то в качестве последовательности рангов с равными шансами может появиться любая перестановка чисел от 1 до m+n. Число таких перестановок равно (m+n)!, поэтому вероятность каждой равна . Заметим, что этот результ никак не зависит от распределения самих наблюдений.

Посмотрим, как изменяется распределение вероятностей среди ранговых последовательностей (т.е. среди перестановок) при отступлениях от однородности выборок. В качестве нарушений однородности мы будем рассматривать те же ситуации, что и при обсуждении критерия Манна-Уитни в предыдущем пункте: левосторонние альтернативы и правосторонние альтернативы F  G. Для правосторонних альтернатив , то есть наблюдения из второй группы имеют тенденцию превосходить наблюдения из первой. Поэтому ранг наблюдений из второй группы чаще будет принимать значения из правой части ряда чисел 1,2,..., m + п. Если же отступление таково, что , то ранги игреков чаще будут принимать значения из левой части ряда чисел 1,2,..., m+n. Переход от рангов игреков к их сумме позволяет резче отметить эти закономерности.

Таким образом, ранги в какой-то мере способны характеризовать, например, положение одной выборки по отношению к другой и в то же время они не зависят от неизвестных нам распределений выборок х и у. Это обстоятельство и легло в основу ранговых методов, широко применяемых в настоящее время в различных задачах. Вернемся к непосредственному обсуждению критерия Уилкоксона.

Назначение. Критерий Уилкоксона используется для проверки гипотезы об однородности двух выборок. Нередко одна из выборок представляет характеристики объектов, подвергшихся перед тем какому-то воздействию (обработке). В этом случае гипотезу однородности можно назвать гипотезой об отсутствии эффекта обработки.

Данные. Рассматриваются две выборки и , объемов m и п. Обозначим закон распределения первой выборки через F, а второй — через G.

Допущения. 1. Выборки и независимы между собой.

2. Законы распределения выборок F и G непрерывны.

Гипотеза. В введенных выше обозначениях гипотезу об однородности выборок можно записать в виде Н : F = G.

Метод. 1. Рассмотрим ранги игреков в общей совокупности выборок х и у. Обозначим их через .

2. Вычислим величину

,

называемую статистикой Уилкоксона.

3. Зададим уровень значимости  или выберем метод, связанный с определением наименьшего уровня значимости, приведенный ниже.

4. Для проверки Н на уровне значимости  против правосторонних альтернатив найдем по таблице верхнее критическое значение W(, m, n), т.е. такое значение, для которого

Гипотезу следует отвергнуть против правосторонней альтернативы при уровне значимости , если .

5. Для проверки H на уровне значимости  против левосторонних альтернатив , необходимо вычислить нижнее критическое значение статистики W. В силу симметричности распределения W нижнее критическое значение есть n(m+n+1)-W(, m, п). Гипотеза H должна быть отвергнута на уровне значимости  против левосторонней альтернативы, если .

6. Гипотеза H отвергается на уровне 2 против двусторонней альтернативы , если

или .

Напомним, что альтернативы должны выбираться из содержательных соображений, связанных с условиями получения экспериментальных данных.

7. Более гибкое правило проверки Н связано с вычислением наименьшего уровня значимости, на котором гипотеза Н может быть отвергнута. Для разных альтернатив речь идет о вычислении вероятностей:

Гипотеза отвергается, если соответствующая вероятность оказывается малой.

Приближение для больших выборок. На практике часто приходится сталкиваться с ситуацией, когда объемы выборок т и п выходят за пределы, приведенные в таблицах. В этом случае используют аппроксимацию распределения W предельным распределением статистики W при и . Перейдем от величины W к . Ниже будет показано, что . Так же можно показать, что . Доказано, что в условиях H, при допущениях 1 и 2 и при больших т, п случайная величина W^* распределена приблизительно по нормальному закону с параметрами (0, 1).

Обозначим через z_ верхнее критическое значение стандартного нормального распределения. Его можно найти с помощью таблицы квантилей нормального распределения для любого 0 <  < 0.5. Благодаря симметрии распределения нижнее критическое значение равно - z_. Правило проверки H перефразируем так:

• отвергнуть H на уровне  против альтернативы , если ;

• отвергнуть H на уровне  против альтернативы , если ;

• отвергнуть H на уровне 2 против альтернативы , если .

Правило, связанное с вычислением наименьшего уровня значимости, при использовании нормального приближения выглядит так: отвергнуть H (против соответствующих альтернатив), если оказывается малой вероятность для альтернативы , для альтернативы , и для альтернативы , где Ф(u) — функция нормального распределения (функция Лапласа), равная

.

Функция нормального распределения и ей обратная, которая называется функцией квантилей стандартного нормального распределения, подробно табулированы. Упомянутое ранее верхнее критическое значение z_ с помощью функции Ф можно определить как решение уравнения

Замечание. Указанное выше нормальное приближение для вычисления критических значений статистики W хорошо действует даже для небольших значений m и п, если только  не слишком мало. (Так, для т = п = 8 приближенные квантили практически не отличаются от точных.)

Обсуждение. Рассмотрим подробнее свойства статистики W и соображения положенные в основу критерия Уилкоксона.

Область определения. Случайная величина W может принимать все целые значения от минимального значения до максимального . Минимальное значение W мы получаем, когда рангами игреков служат (в той или иной последовательности) числа 1, 2,... ,п. Максимальное значение W возникает, когда этими рангами служат m+1, m+2,..., т+п.

Заметим, что W не изменится, если произвольно переменить порядок следования чисел, служащих рангами игреков (как не изменится и при перенумерации самих игреков). Чтобы упростить обсуждение, можно поэтому говорить далее о рангах игреков, упорядоченных по возрастанию. Пусть обозначают именно упорядоченные ранги, так что .

Распределение вероятностей. Статистика Уилкоксона была определена нами как сумма (упорядоченного) набора рангов игреков . Вероятность каждого такого упорядоченного набора при выдвинутой гипотезе Н — одна и та же и равна . Таким образом, при гипотезе Н распределение W не зависит от закона распределения выборок х и у, так как от них не зависит распределение упорядоченной последовательности рангов. Для каждой пары (m, n) распределение W можно рассчитать. Покажем на примере, как это делается.

Пусть m = 3 и n = 2. Вычислим число всех возможных пар рангов игреков. Оно равно Следовательно, вероятность каждого упорядоченного набора рангов равна 0.1. Выпишем всевозможные наборы рангов S₁, S₂ и соответствующую им сумму:

S1, S2	1.2	1.3	1.4	1.5	2.3	2.4	2.5	3.4	3.5	4.5
W	3	4	5	6	5	6	7	7	8	9

Таким образом, получаем следующее распределение W:

W	3	4	5	6	7	8	9
P(W)	0.1	0.1	0.2	0.2	0.2	0.1	0.1

Отметим, что распределение W симметрично относительно точки — середины отрезка . Из этого свойства легко вывести, что .

Рассмотрим случайную величину . Согласно симметрии закона распределения относительно точки , вероятность , что эта величина примет некоторое значение k, равна вероятности , что она примет значение -k. Согласно определению математического ожидания, . Учитывая, что математическое ожидание разности равно разности математических ожиданий, а математическое ожидание константы равно самой константе, получат .

Распределение статистики W при нарушении гипотезы. Чтобы оправдать сделанный выше выбор критических событий (критериев) для проверки Н против рассмотренных альтернатив, надо изучить распределение статистик U и W при этих альтернативах. Когда F и G не одинаковы, распределения U и W уже не свободны от их влияния. Поэтому точно вычислить и указать распределения U и W можно (в принципе) только для каждой конкретной пары F и G. Тем не менее, характер изменения распределений статистик U и W при переходе от гипотезы к альтернативам — не всем, но некоторым, — установить можно. Это легко сделать для односторонних альтернатив. Например, когда (правосторонняя альтернатива), распределение вероятностей W «перетекает» от середины к правому концу того множества значений, которое может принимать W. Для левосторонних альтернатив аналогичное «перетекание» вероятности происходит влево — тем сильнее, чем больше отличается от 0.5.

На рис. 1 мы попытались наглядно представить это положение, условно представляя распределение статистики W при гипотезе и при альтернативах с помощью плотностей, — хотя искомые распределения дискретны и плотностей не имеют. Но так получается выразительнее. (При желании можно считать, что нарисованные непрерывные кривые изображают что-то вроде огибающих графиков дискретных вероятностей.)

Рис. 1

Из рис. 1 ясно, что гипотеза Н должна отвергаться при слишком больше или при слишком малых значениях W в зависимости от того, какие альтернативы мы рассматриваем. При том выборе критериев, который был описан выше их мощность возрастает при удалении от 0.5. Это правило и лежит в основе описанного выше метода.

Связь со статистикой Манна-Уитни. Нетрудно проверить, что для всех m, n: . Это соотношение показывает эквивалентность статистик U и W. Поэтому их применения приводят к одинаковым результатам.

Совпадения. Мы описали критерий Уилкоксона для проверки гипотезы об однородности двух выборок в условиях, когда функции распределений данных непрерывны и, тем самым, в выборках не должно быть совпадающих наблюдений. Однако на практике совпадающие наблюдения — не редкость. Чаще всего это происходит не потому, что нарушается условие непрерывности, а из-за ограниченной точности записи результатов измерений (например, рост человека обычно измеряется с точностью до 1 см). Применение критерия Уилкоксона к таким данным приводит к приближенным выводам, точность которых тем ниже, чем больше совпадающих значений.

Когда среди наблюдений встречаются одинаковые, им приписываются средние ранги. По определению, средний ранг числа в совокупности чисел есть среднее арифметическое из тех рангов, которые были бы назначены и всем остальным значениям, совпадающим с , если бы они оказались различными. После такого назначения рангов применяются описанные ранее процедуры.

Упомянутые группы одинаковых наблюдений называют связками. Количество элементов в связке называют ее размером. Наличие связей влияет на асимптотические распределения статистики Уилкоксона. Так, при использовании нормальной аппроксимации следует в формуле для вычисления W^* заменить DW на

,

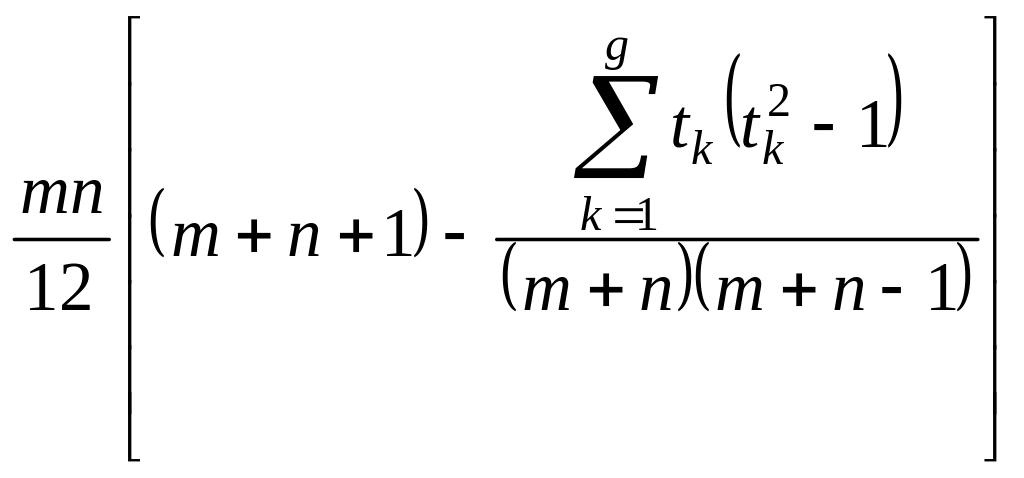где — размеры наблюденных связок среди игреков, g — общее число связок среди игреков. Наблюдение, не совпавшее с каким-либо другим наблюдением, рассматривается как связка размера 1, и в формуле, заменяющей DW не учитывается.

При больших по размеру связках и (или) большом их числе применение критерия Уилкоксона сомнительно.