5.4. Понятие о доверительных границах для средних

При использовании результатов выборочного наблюдения нельзя ограничиваться только приближенным равенством для характеристики связи между генеральной и выборочной средней.

Важно еще установить границы ошибки выборки . В связи с этим вводится понятие о доверительных границах для средних.

В качестве критерия здесь принимается так называемая доверительная вероятность Р, отвечающая условию

, или .

Число Р выбирается произвольно, но достаточно близким к 1, и этим характеризуется надежность неравенства .

Применяя для выражения преобразованную форму интегральной теоремы Лапласа, будем иметь

,

где , а (значение t находится по таблице значений Ф(х) из условия Ф(t)=Р, которое задано).

Этим определяется доверительная оценка средней условием

с надежностью Р.

Поэтому, если дана достаточно большая выборка из генеральной совокупности, определяющей случайную величину X, у которой известны математическое ожидание а и дисперсия , то с вероятностью Р можно принять, что выборочная средняя удовлетворяет неравенству

Отсюда следует, что средняя находится в доверительном интервале .

Таким образом, для вычисления доверительных границ для выборочной средней с надежностью Р=Ф(t) следует найти t=t(Р), а затем вычислить .

По найденному значению  и определяются доверительные границы для вычисленной выборочной средней в виде

.

На практике требуется вычисление доверительных границ не для выборочной средней (поскольку генеральная средняя случайной величины М(Х)=а неизвестна), а для генеральной средней. Поэтому построение соответствующей задачи должно быть таким: по данным выборочного наблюдения отыскиваются выборочная средняя , или средняя доля признака, и выборочная дисперсия ;

по заданному значению Р=Ф(t) отыскивается t=t(Р);

определяется средняя квадратическая ошибка выборки ;

определяется предельная ошибка выборки ;

по этому значению  устанавливаются доверительные границы для генеральной средней

.

5.5. Примеры математической обработки данных выборочного наблюдения

Приведенные в предыдущих параграфах сведения позволяют решить ряд примеров, связанных с результатами выборочного наблю дения.

Пример 2. Для определения средней урожайности пшеницы на площади 10000 га определена урожайность на 1000 га. Результаты выборочного обследования представлены в виде следующего распределения:

Урожайность в ц с га	Количество га
11 – 13 13 – 15 15 – 17 17 – 19	150 200 450 200
Итого	1000

Найти вероятность того, что средняя урожайность пшеницы на всем массиве отличается от средней выборочной не более чем на 0,1 ц, если выборка: а) повторная, б) бесповторная.

Решение. Вычислим среднюю арифметическую и дисперсии данного в условии распределения (это будут выборочная средняя и выборочная дисперсия).

За значение признака нужно принять середины интервалов В результате получим

.

Для нахождения вероятности искомого события применяем формулу

,

в которой . Найдем среднюю квадратическую ошибку .

Для повторной выборки по формуле (1), в которой , а п= 1000, получим

,

а в случае бесповторной выборки имеем по формуле (3)

.

Если выборка повторная, то вычисление искомой вероятности дает

Если же выборка бесповторная, то искомая вероятность

Пример 3. Нз партии, содержащей 8000 деталей, было проверено 1000 деталей. Среди них оказалось 4% нестандартных. Определить вероятность того, что доля нестандартных деталей во всей партии отличается от их доли в выборке (=0,04) не более чем на 0,015, если выборка: а) повторная, б) бесповторная.

Решение. В соответствии с формулой (2) при =0,04, п = 1000 средняя квадратическая ошибка повторной выборки

.

Если выборка бесповторная, то в соответствии с формулой (4) при значениях =0,04, п = 1000 и N= 8000, средняя квадратическая ошибка .

Отсюда искомая вероятность определяется так:

а) при повторной выборке

б) при бесповторной выборке .

Пример 4. При условиях приведенного выше примера 2 найти границы, в которых с вероятностью 0,9973 заключена урожайность на всем массиве.

Решение. По таблице значений функции Ф(х) находим, что Ф(3)=0.9973. Следовательно, при соотношении

, или

можно, зная значения  и для повторной и для бесповторной выборки, найти  (предельную ошибку выборки):

а) если выборка повторная, то

;

б) если выборка бесповторная, то

.

Таким образом, с вероятностью 0,9973 средняя урожайность (в ц) на всем массиве заключена в границах 15,4±0,18, т. е. от 15,4-0,18 = 15,22 до 15,4+0,18=15,58, если выборка повторная, и в границах 15,4±0,17, т. е. от 15,4-0,17=15,23 до 15,4+0,17=15,57, если выборка бесповторная.

Пример 5. Из партии, содержащей 8000 деталей, было проверено 1000 деталей. Среди них оказалось 4% нестандартных. Определить границы, в которых с вероятностью 0,9545 заключена доля нестандартных деталей во всей партии, если выборка: а) повторная, б) бесповторная.

Решение. По таблице значений функции Ф(х) находим, что . Следовательно, приходим к равенству , где  — средняя квадратическая ошибка. В примере 3 (см. выше) мы вычислили, что она равна 0,0062, если выборка повторная, и 0,0059, если выборка бесповторная. Поэтому предельная ошибка выборки

, если выборка повторная;

, если выборка бесповторная,

Теперь можно найти искомые границы. Они буду таковы:

0,04±0,0124, т. е. от 0,0276 до 0,0524

(или от 2,76% до 5,24%), если выборка повторная, и

0,04±0,0118, т. е. от 0,0282 до 0,0518

(или от 2,82% до 5,18%), если выборка бесповторная.

Если требуется определить необходимый объем (п) повторной выборки, при котором с заданной надежностью (Р) отклонение выборочной средней или доли от генеральной не превысило данной предельной ошибки (), то значение п отыскивается из соотношения . Здесь t определяется по таблице из условия , a  — по одной из четырех формул. В частности, при определении средней признака искомый объем находится в виде , а при определении доли признака — в виде или .

Пример 6. Из партии в 1000 единиц готовой продукции производится повторная выборка для определения доли брака. Найти тот объем этой выборки, при котором с вероятностью Р=0,99 гарантируется ошибка не свыше 0,1.

Решение. Здесь . Значению по таблице значений Ф(х) соответствует . При заданном имеем . Значение п следует найти из соотношения . Но в условии нет значения доли брака. Поэтому следует использовать наибольшее значение pq=0,25. Это приводит к соотношению , откуда .

Если надо установить объем выборочной совокупности при бесповторной выборке, то из формул (3) и (4)

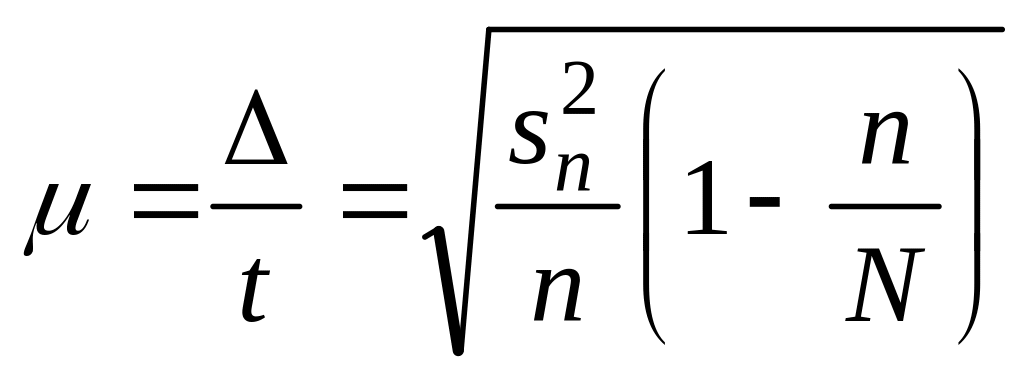и

получаются следующие выражения для этого объема в бесповторной выборке:

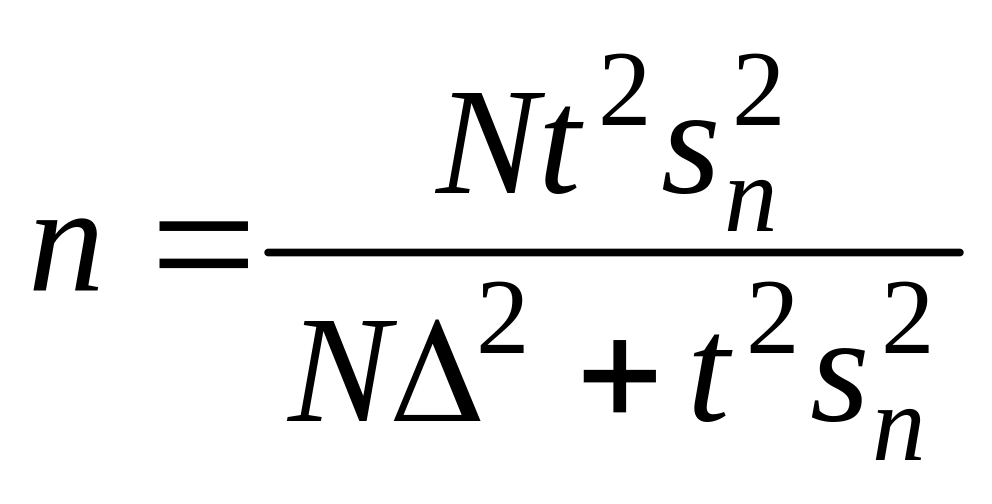(при определении средней признака)

и

(при определении доли признака).

Пример 7. Найти объем выборки из партии в 6000 прецизионных приборов, при котором можно с вероятностью Р=0,890 утверждать, что отклонение доли точных приборов в выборке от вероятности их изготовления р=0,4 не превысит 0,02: а) при повторной выборке и б) при бесповторной выборке.

Решение. Здесь дает по таблице значений Ф(х) t=1,6. Предельная ошибка выборки по условию . Отсюда

а) при повторной выборке применяется формула , что дает:

б) при бесповторнои выборке применяем формулу , что дает: