3.4. Нормальный закон распределения и понятие о теореме Ляпунова
О непрерывной случайной величине говорят, что она подчинена нормальному закону распределения или называется нормально распределенной, если плотность ее вероятности определяется формулой
.
Здесь а и
— параметры
распределения. Можно показать, что
— среднее значение,
а —
среднее квадратическое отклонение
этой случайной величины.
В частном случае при а=0 эта плотность выражается функцией
.
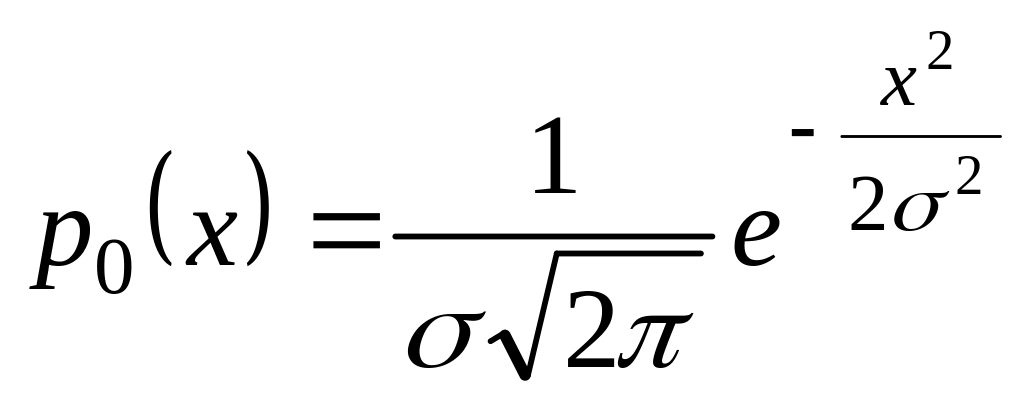График этой функции представляет кривую вероятностей и характеризуется следующими особенностями:
1) кривая пересекается с
осью Оу в точке
являющейся точкой максимума заданной
функции, так как в точке х=
0 обращается в нуль ее первая
производная
;
2) с осью Ох кривая не
пересекается, но с возрастанием
асимптотически приближается к ней;
3) кривая симметрична
относительно оси Оу, так как
- четная функция;
4) по второй производной
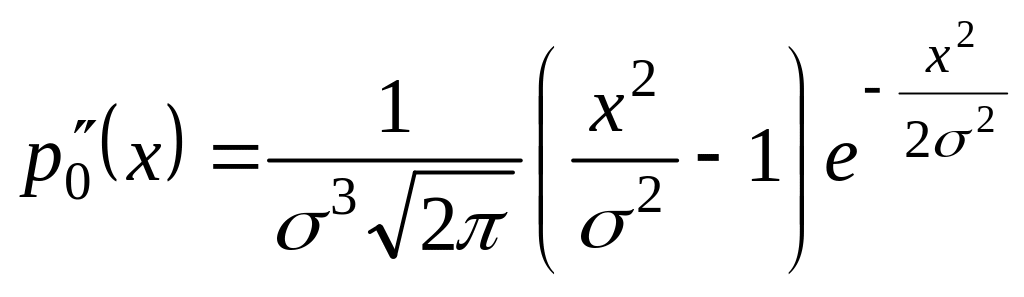
определяются две точки перегиба кривой с координатами:
и
.
Здесь важно отметить, что именно параметр определяет абсциссы точек перегиба кривой вероятностей.
Построенная по этим результатам исследования кривая дается на рис. 11.
С изменением значения
меняются ординаты вершины и точек
перегиба кривой, а это соответственно
влияет на ее конфигурацию. Наглядное
отражение этих изменений дает рис.
12, на котором наряду
с кривой при
помещены еще две кривые — при
и при
.
Кривая с параметром
принята здесь за основную, а другие
получены преобразованием основной
методом сжатий и растяжений. Большему
значению
соответствует большая вытянутость
кривой вдоль оси Ох и большее сжатие
вдоль оси Оу, и наоборот. Это вполне
согласуется с тем, что при большем
значении имеет место большее рассеяние
значений случайной величины относительно
центра рассеяния М(Х).
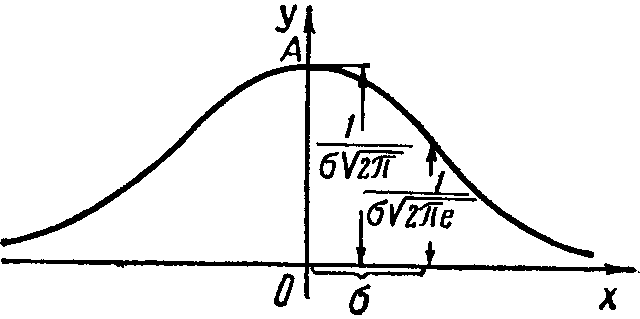
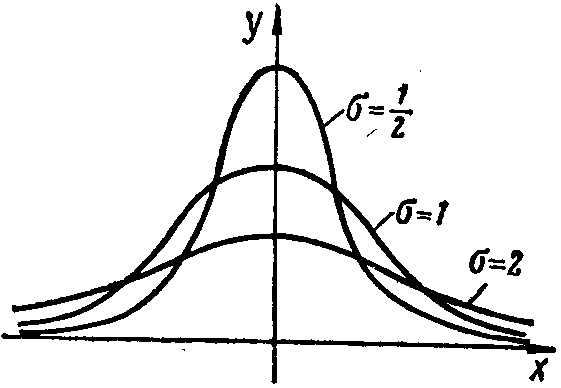
Рис 11 Рис. 12
При
кривые нормального распределения,
заданные плотностью
,
характеризуются горизонтальным сдвигом на а ед. масштаба по сравнению с только что рассмотренными кривыми при тех же значениях параметра . Сама же форма кривых при этом смещении остается без изменения.
Наиболее общий случай нормального распределения имеет место при систематических отклонениях в стрельбе, в измерениях и в других наблюдениях.
Закон нормального распределения имеет в теории вероятностей исключительно важное значение. В сферу его применения включаются не только отдельные случайные величины, но и суммы любого числа независимых случайных величин, распределенных по нормальному закону (соответствующая теорема сложения для нормального распределения доказывается в подробных курсах теории вероятностей). Обработка результатов наблюдения в предположении, что они распределены по нормальному закону, легко доводится до конца с помощью простых правил операций с нормально распределенными величинами.
Более того, оказывается, что закон распределения суммы независимых величин при довольно широких предположениях о законах распределения отдельных слагаемых стремится к нормальному закону, если число слагаемых неограниченно возрастает.
Первое доказательство этого утверждения для независимых повторных испытаний в биномиальном распределении составляет содержание так называемой предельной теоремы Муавра.
В дальнейшем было выяснено, но долгое время оставалось недоказанным, что этот результат имеет место и при гораздо более общих условиях.
Разрешение этого вопроса дает центральная предельная теорема, которая составила предмет научных изысканий ряда крупных математиков, начиная с Лапласа, и строгое доказательство которой было дано А. М. Ляпуновым в 1901 г.
Сущность этой теоремы заключается в том, что при некоторых общих условиях сумма п независимых случайных величин, заданных произвольными распределениями, имеет распределение, которое по мере возрастания числа п стремится к нормальному.
Некоторая конкретизация упомянутых здесь общих условий позволяет так сформулировать теорему Ляпунова.
Если имеется п независимых случайных величин
с математическими ожиданиями
и с дисперсиями
причем отклонения всех случайных
величин от их математических ожиданий
не превышают по абсолютной величине
одного и того же числа
:
,
а все дисперсии ограничены одним и тем же числом С:
,
то при достаточно большом п сумма
случайных величин
,
т. е.
будет подчинена закону распределения,
cколь угодно
близкому к закону нормального
распределения.
Упражнения
1, По таблице распределения случайной величины
|
0 |
1 |
2 |
3 |
4 |
|
0,1 |
0,3 |
0,3 |
0,2 |
0,1 |
определить ее среднее значение, среднее отклонение и среднее квадратическое отклонение.
Отв.
2. Вероятность попадания
из орудия в данную цель при одном выстреле
.
Составить таблицу распределения числа
попаданий при 7 выстрелах;
определить математическое ожидание и
дисперсию этой случайной величины.
Отв.
3. Две независимые случайные величины Х и Y заданы слсдующими табцами распределения:
|
2.5 |
6 |
8.3 |
|
|
5.2 |
7.6 |
|
0.3 |
0.5 |
0.2 |
|
|
0.6 |
0.4 |
Составить таблицы распределения случайных величин X+Y и XY и проверить справедливость свойств о математическом ожидании суммы и произведения случайных величин.