19) Распространение плоских эмв в однородных проводящих средах

К проводящим (поглощающим) относятся среды, обладающие конечной проводимостью γ. Волновые уравнения (уравнения Гельмгольца) для векторов Е и Н:

φе – угол диэлектрич. потерь.

Решение волн. ур-й для комплексных амплитуд данных волн:

Поле в однородной проводящей среде обладает следующими особенностями

1.векторы Е и Н сдвинуты по фазе на угол, равный: ,(вектор магнитного поля отстает);

2. множитель е-αz указывает на экспоненциальное ослабление поля в направлении распространения волны, что связано с потерями энергии на нагрев среды;

3. длина волны определяется действительной частью комплексного коэффициента распространения, коэффициентом фазы

, . И сдвиг фаз вектров Е и Н достиг максим. велич. при .

Vф=f( . Явление зависимости скор-ти распр-я от частоты наз-ся дисперсией.

. Когда энергия поля высокой частоты проникает в хороший проводник поверхностн. эффект (скин-эффекта), заключающегося в том, что амплитуды объемной плотности тока и полей Е и Н при удалении от поверхности проводника уменьшаются по экспоненциальному закону е-αх, и тем резче, чем выше частота. При этом поперечное сечение проводника, по которому проходит основная часть тока, мало и уменьшается с ростом частоты. За счет этого увеличивается сопротивление проводника току высокой частоты и, следовательно, растут тепловые потери.

Расстояние, на котором амплитуды поля и объемной плотности тока падают в "е" раз, называется глубиной проникновения.

Сопротивл-е проводн. поверхн. току хар-ся поверхн. сопре-ем R. С целью уменьшения сопр-я токам высок чатсоты токонес. поверхн. обр-ся по высок. классу частоты - полируются.

20) Распространение плоских эмв в однородном изотропном идеальном

диэлектрике

Рассмотрим распространение плоских волн в однородной изотропной среде с параметрами εа, μа и проводимостью γ=0 (идеальный диэлектрик).

Плоская волна, распространяющаяся в положительном направлении оси z, может быть записана в комплексной форме:

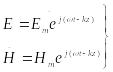(1)

Интересующие нас физические величины волн характеризуются вещественной частью комплексных выражений (1). Поэтому для наглядного представления плоских волн выделим именно эти части выражений:

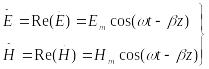(2)

Выражения (2) были получены в предположении, что плоская волна распространяется в однородном изотропном идеальном диэлектрике (у идеального диэлектрика α=0, следовательно, ).

Над волнами, записанными в форме комплексных амплитуд, можно производить только линейные операции, при расчетах плотности потока энергии и других нелинейных операциях над комплексными амплитудами необходимо переходить от комплексных амплитуд к вещественным составляющим полей (2). Выражения (2) описывают гармоническую плоскую волну, распространяющуюся вдоль оси z (рис). Векторы напряженности электрического и магнитного полей плоской волны синфазны и осциллируют вдоль взаимно перпендикулярных направлений в плоскости, перпендикулярной направлению распространения волны. Такие волны являются поперечными. Если фаза φ=ωt-βz зависит от времени и от координаты, то поле является полем волны, бегущей вдоль координаты z в сторону z > 0. Фаза поля, бегущего от возбудителя в сторону z > 0, с ростом координаты z уменьшается, так как волновой процесс в далеких точках запаздывает по фазе. Если фаза поля волны зависит только от времени, то такое поле не переносит электромагнитной энергии в каком-либо направлении и является полем стоячей волны.

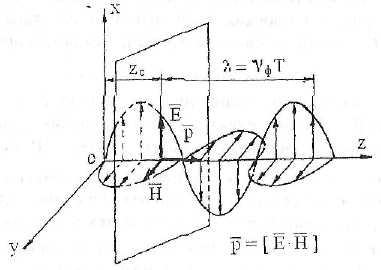
Рис. Мгновенная картина распределения напряженности электрического и магнитного полей вдоль направления распространения плоской волны. Во времени картина поля перемещается в пространстве с фазовой скоростью Vф вдоль оси z