16) Стационарное магнитное поле (система уравнений , прямая задача ,

векторный потенциал , граничные условия , индуктивность ,энергия )

Стационарным магнитным полем называется магнитное поле постоянного тока. Это поле соответствует режиму установившегося движения зарядов.

Уравнения стационарного магнитного поля вытекают из 1-го и 3-го уравнений электродинамики и материального уравнения и имеют вид:

з акон полного тока:

в дифференциальной форме

в интегральной форме:

З акон непрерывности магнитного поля:

в дифференциальной форме:

в интегральной форме:

м атериальное уравнение:

Из уравнений следует, что в отличие электростатического поля стационарное магнитное поле является вихревым.

:Прямая задача стационарного магнитного поля заключается в том, что по известной величине тока и его распределению требуется найти магнитное поле. Наиболее просто эта задача решается при помощи потенциалов стационарного магнитного поля. Векторный потенциал магнитного поля является частным случаем векторного электродинамического потенциала при частоте ω = 0:

Функция называется векторным потенциалом магнитного поля.

, те. поле вектора явл-ся вихревым. Получ. соотнош. позвол. однознач. опред. вектор. потенц.

Гранич. усл. для стац магн. поля – частн. случ. гран. усл. электродин. для случая, когда все велич. не завис. от времени:

Индуктивность является важным электромагнитным параметром, электромагнитных систем и электрических цепей. Она определяется путем расчета магнитного поля токов.

Собственная индуктивность контура представляет собой отношение полного магнитного потока к вызвавшему его току: L=Фсц/J, Г,

где Фсц – потосцепление (это полн магн. поток через пов-ть, натян. на контур стоком)

Из теоремы Умова-Пойнтинга следует, что энергия, запасенная в магнитном поле, определяется формулой

А формула для энергии поля катушки индуктивности:

17) Магнитостатика

Магнитостатика изучает поля постоянных магнитов. В областях, где нет свободных токов

( = 0), уравнения и граничные условия стационарного магнитного поля принимают следующий вид:

1 и 2 ур-я опис. магнитостат. поле. В этом случае нет ни источников магнитного поля, ни вихрей. Поэтому в магнитостатике магнитное поле можно получить лишь за счет намагниченности среды. Намагниченность среды обусловлена молекулярными (атомарными) токами. Каждый электрон, вращаясь вокруг ядра, создает магнитный атомарный (молекулярный) момент. Количество намагниченности среды характеризуется вектором намагниченности М.. Магнитостат. поле явл-ся безвихревым.

Магнитное поле является полем градиентов скалярного магнитного потенциала (см. ф-лу ниже):

Магнитостат. потенц. удовлетв. ур-ю Лапласа:

В обл-х пр-ва, где , магн. поле рассм. как потенциальн. И тогда величина скалярн. магнитостат. потенц. не завис. от формы пути, а зависит лишь от полож. точек.

18) Плоская однородная волна и ее параметры

Плоские волны являются предельным случаем сферических волн при стремлении радиуса сферы к бесконечности (R →∞). Фронт волны представляет собой геометрическое место точек поля с одинаковой фазой: у плоской волны (рис.1.2) одной из этих поверхностей является плоскость 0 z = z , перпендикулярная направлению распространения волны. У плоской однородной волны поверхность равных фаз и равных

а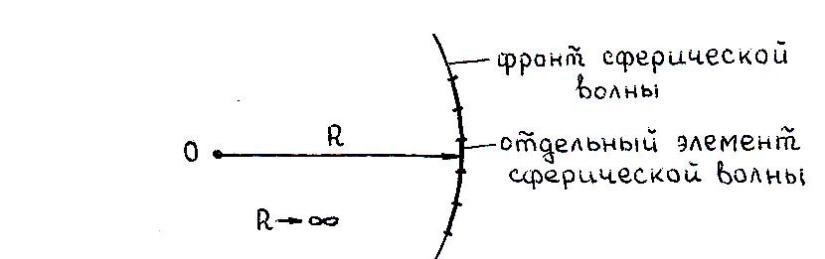 мплитуд совпадает. Любой волновой процесс характеризуется длиной волны λ , коэффициентом фазы β , фазовой ф ν и групповой гр ν скоростями. 1) Под длиной волны понимается расстояние между двумя точками поля бегущей волны, разность фаз которых равна 2π.2) Фазовая скорость ф ν это скорость перемещения фронта волны. Фазовая скорость может быть больше скорости света, т.к. она не представляет собой скорости переноса энергии электромагнитного поля. 3) Групповая скорость характеризует скорость перемещения весьма узкополосного сигнала и, следовательно, скорость перемещения энергии поля такого сигнала. Отсюда следует, что групповая скорость не может быть больше скорости света. Коэффициент фазы β показывает набег фазы бегущей волны на единицу длины. Рассмотренные величины, связаны между собой следующим образом: