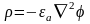14) Электродинамические потенциалы и волновые уравнения

Волновое уравнение для магнитного поля:

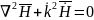
Волновое уравнение для электрического поля:

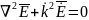
Эти уравнения вводятся для облегчения решения задач по определению полей.

В отличие от уравнений ЭД волновые уравнения являются уравнениями второго порядка. Эти уравнения содержат в себе только одно неизвестное поле и называются однородными, т.к. их правая часть равна 0. Решениями этих уравнений являются волны.

Векторный ЭД потенциал: и

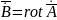
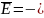, где 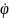– скалярный ЭД потенциал.

ЭД потенциалы вводятся как вспомогательные функции для облегчения решения задачи по определению полей (решение диф.ур. сводится к определению скалярной или векторной функции, имеющей меньшее число проекций, чем искомое поле).

15) Электростатика (система уравнений , скалярный потенциал , граничные

условия , прямая и обратная задачи , емкость, энергия )

Система ур-й электростатики в дифф. форме:

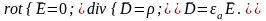
В интегральной форме:

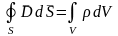
Из этих ур-й вытекает, что электростат поле явл. безвихревым.

Часто необходимо опр-ть потенц поля в дан. точке, если изв-на его напр-ть, тогда:

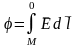. Исходя из ф-лы: скалярный потенциал в произвольной точке М -это линейный интеграл от вектора напряженности электрического поля Е , взятый от точки М до некоторой точки 0 , принятой за начало отсчета потенциала. Так как электростатическое поле потенциально, то потенциал поля зависит от координаты точки и не зависит от формы пути интегрирования. Последнее выражение позволяет выяснить физический смысл потенциала. Т.к. напряженность электрического поля равна силе, с которой поле действует на единичный положительный заряд, то произведение 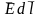, стоящее под знаком интеграла, равно работе, совершаемой полем по перемещению этого заряда на пути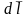 .Т.е. потенциал поля в точке М равен работе, которую совершит поле при переносе единичного положительного точечного заряда из точки М в точку О, принятую за начало отсчета потенциала.

Граничные условия электростатики представляют собой частный случай граничных условий электродинамики для полей, не зависящих от времени.

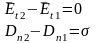
Если на границе раздела нет поверхностных зарядов (σ = 0), то граничные условия упрощаются и принимают вид:

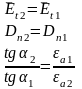
Чем больший заряд нужно сообщить проводнику, тем больше емкость проводника. Емкость определяется как отношение заряда проводника к его потенциалу: С=Q/φ, Ф. Для создания емкости обычно используют систему из двух проводников, заряды которых равны по величине и противоположны по знаку. Такая система называется конденсатором.

Тогда емкостью конденсатора также опр-ся форм-й:

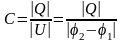, где 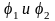- потенц. провод-в, U- разность потенциалов.

Таким образом, емкость конденсатора - это величина, равная отношению величины заряда одного из проводников к величине разности потенциалов между ними.

Величина емкости системы связана с энергией электрического поля этой системы., энергия We электрического поля во всем объеме, где оно существует, определяется соотношением .

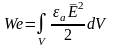А формула для опред-я энерг. поля конденсатора будет равна:

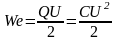, т.к Q=CU.

Задача опр-я поля по задан. зарядам наз-ся прямой задачей электростатики. При ее решении удобно использовать готовые решения уравнения Пуассона, позволяющие сразу найти поле по заданным зарядам.

Обратной задачей электростатики называется задача определения величины зарядов и их распределения в объеме и на поверхностях ! проводников, если известно поле. Эта задача также решается с помощью уравнения Пуассона и граничных условий. Объемная плотность зарядов в объеме, где имеется поле, определяется формулой