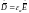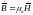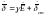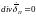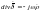- •Электрические заряды и токи
- •Собственные векторы эмп
- •8) Комплексная диэлектрическая проницаемость . Диэлектрики и
- •9) Граничные условия электродинамики в общем виде
- •10) Граничные условия на поверхности идеального проводника
- •11) Теорема Умова – Пойнтинга
- •12) Вектор Умова – Пойнтинга
- •13) Теорема единственности решения основных уравнений
- •14) Электродинамические потенциалы и волновые уравнения
- •15) Электростатика (система уравнений , скалярный потенциал , граничные
- •16) Стационарное магнитное поле (система уравнений , прямая задача ,
- •17) Магнитостатика
- •18) Плоская однородная волна и ее параметры
- •19) Распространение плоских эмв в однородных проводящих средах
- •20) Распространение плоских эмв в однородном изотропном идеальном
- •21) Поверхностный эффект
- •22) Виды поляризации эмв
- •23) Отражение и преломление плоских эмв
- •24) Структура поля над проводящей плоскостью
- •25) Двухплоскостной волновод
- •26) Открытые и закрытые линии передачи . Требования к линиям передачи
- •27) Поле различных типов волн в волноводах
- •28) Методика построения картин поля в волноводе (примеры использования
- •29) Режимы в волноводах
- •30) Затухания в волноводах
- •31) Отражения в линиях передачи и необходимость их согласования
- •32) Выбор размеров волновода по заданному диапазону рабочих частот и
- •33) Предельная и допустимая мощности в волноводе
- •34) Коэффициент полезного действия линий передачи
- •35) Максимально допустимая длина волноводной линии передачи
- •36)Методы возбуждения поля в волноводах
- •37) Линии передачи с волной т (основные характеристики , достоинства и
- •39) Коаксиальная лп
- •40) Полосковые лп
- •41) Назначение и виды резонаторов
- •42) Поля различных типов колебании в резонаторах и правила их
- •43) Собственные и резонансные частоты резонаторов
- •44) Запасенная в резонаторе эм энергия и расчет потерь
- •45) Добротность резонаторов
- •46) Эффект Фарадея
- •47) Явление ферромагнитного резонанса
- •49) Формула идеальной радиопередачи
- •50) Область пространства, существенная при ррв. Метод зон Френеля
- •51) Влияние земной поверхности на ррв
- •52) Тропосфера и ее влияние на ррв
- •53) Ионосфера и ее влияние на ррв
- •60) Электромагнитная безопасность
Электрические заряды и токи
Электрические заряды и токи. Наименьшим элементарным электрическим зарядом является электрон. Его заряд отрицателен и имеет величину q = -1.6-10^-19 Кл. Кроме электрона существуют положительно заряженные частицы, такие как протоны и позитроны. В макроскопической теории электромагнитного поля не рассматриваются отдельные электроны, а изучается их совокупность как непрерывное распределение заряженных частиц. При таком подходе будем считать, что даже в элементарно малом объеме dV имеется достаточно много элементарных частиц и что поэтому справедлив макроскопический подход. Электрически заряженным телом или объемом V называется тело или
объем, обладающий избытком отрицательных или положительных частиц. Реальные электрические заряды ∆Q всегда занимают некоторый объем ∆V поэтому, строго говоря, заряды имеют объемное распределение. Однако практически мы часто встречаемся с распределением зарядов в очень тонком слое, например, на поверхности проводника ∆S; или с зарядами, распределенными вдоль тонкой нити или линии ∆l или с зарядами,
с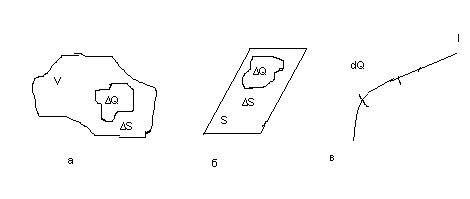 осредоточенными,
в очень малом объеме. В этих случаях
распределение зарядов идеализируется
и возникают понятия поверхностного,
линейного и точечного распределения
зарядов. При объемном распределении
зарядов считают, что заряды распределены
в некотором объеме V (рис.1 а). Примером
объемного распределения зарядов может
служить пучок электронов в электронно-лучевой
трубке, пространственный заряд в
вакуумной лампе, ионосфера. а б в
осредоточенными,
в очень малом объеме. В этих случаях
распределение зарядов идеализируется
и возникают понятия поверхностного,
линейного и точечного распределения
зарядов. При объемном распределении
зарядов считают, что заряды распределены
в некотором объеме V (рис.1 а). Примером
объемного распределения зарядов может
служить пучок электронов в электронно-лучевой
трубке, пространственный заряд в
вакуумной лампе, ионосфера. а б в
Рис. 1. Виды распределения зарядов:
L;
а - объемное; б - поверхностное; в — линейное
В случае поверхностного распределения- зарядов идеализированно считают, что заряды сосредоточены в бесконечно тонком слое на поверхности S (рис1 б). Примером такого распределения может служить распределение
зарядов на поверхности проводника. При линейном распределении зарядов считают, что заряды распределены вдоль бесконечно тонкой нити. Примером такого распределения является тонкая заряженная нить (рис. 1 в).
Собственные векторы эмп
Формально поля определяются заданием в каждой точке рассматриваемой области пространства некоторой скалярной или векторной величины: скалярные и векторные поля. Скалярной величиной называется величина, значение которой характеризуется одним действительным числом, без учета направления или другой какой-либо оценки, например, сопротивление, заряд, температура и др. Векторная величина или вектор зависит от двух элементов разной
природы: числа, характеризующего длину вектора (модуль), и направления вектора. Примерами векторов могут служить напряженность и индукция электрического (магнитного) поля. Скалярное поле графически изображается на плоскости рисунка линиями равного уровня, которые являются геометрическим местом точек равного значения скалярной функции φ = const. В пространстве геометрическое место точек равных значений скалярной функции в общем случае являются поверхностями. Изображают поверхности или линии равного уровня так, чтобы разность значений скалярной функции точки любых двух соседних поверхностей равного уровня была одинаковой величины.
Н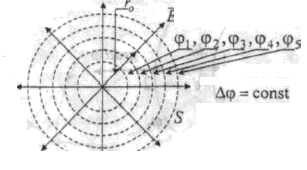 апример,
для скалярного поля электростатического
потенциала φ (рис. 1) эти поверхности
называются эквипотенциальными
(равнопотенциальными) и изображаются
так, чтобы
апример,
для скалярного поля электростатического
потенциала φ (рис. 1) эти поверхности
называются эквипотенциальными
(равнопотенциальными) и изображаются
так, чтобы
Рис. 1. Построение эквипотенциален точечного заряда
Мы видим, что скалярное поле ср порождает векторное поле F = grad φ
Такое векторное поле называется потенциальным, а скалярная функция φ-
потенциалом.
3) Виды сред (в зависимости от свойств параметров среды )
Виды
сред различаются в зависимости от
свойств параметров
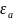 (абсолютная диэлетрическая проницаемость
среды),
(абсолютная диэлетрическая проницаемость
среды),
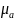 (абсолютная магнитная проницаемость
среды) и
(абсолютная магнитная проницаемость
среды) и
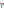 (удельная объемная проводимость
вещества), описанных в материальных
уравнениях.
(удельная объемная проводимость
вещества), описанных в материальных
уравнениях.
4) Материальные уравнения
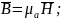
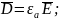
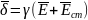 – материальные
уравнения (связывающие векторы ЭМ поля
с параметрами среды).
– материальные
уравнения (связывающие векторы ЭМ поля
с параметрами среды).
5) Система уравнений электродинамики в общем виде

6 )
Следствия из уравнений электродинамики
)
Следствия из уравнений электродинамики
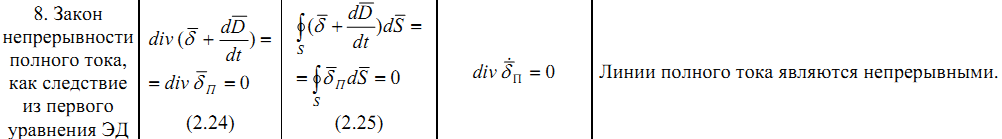
7) Система уравнений электродинамики в комплексной форме
Четыре основных уравнения (Максвелла) |
|
1. Первое уравнение ЭД-закон полного тока |
|
2. Второе уравнение ЭД-закон электромагнитной индукции |
|
3. Третье уравнение ЭД-закон непрерывности магнитного поля |
|
4. Четвертое уравнение ЭД- теорема о потоке вектора электрической индукции |
|
Три уравнения, учитывающие параметры среды |
|
5. |
|
6. |
|
7. Дифференциальная форма обобщенного закона Ома |
|
Два дополнительных уравнения, как следствие из основных |
|
8. Закон непрерывности полного тока, как следствие из первого уравнения ЭД |
|
9. Закон сохранения заряда |
|

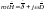
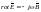
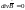 (является
следствием из второго уравнения)
(является
следствием из второго уравнения)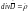 (является
следствием из первого уравнения)
(является
следствием из первого уравнения)