1. Понятие множества. Виды множеств. Числовая ось.

Понятие множества является фундаментальным неопределимым понятием.

Интуитивно под множеством будем понимать собрание определенных вполне различимых объектов, рассматриваемых как единое целое. Отдельные объекты, из

которых состоит множество, называются элементами его. Для обозначения конкретных множеств используются прописные (возможно с индексами) буквы

A, X , A1, X1, для обозначения элементов множества используются строчные (возможно с индексами) буквы x, a, x1,a1. Если x − элемент множества X , то пишут x∈ X (∈− символ принадлежности). Множество, не имеющее ни одного элемента, называют пустым множеством (обозначается Ø). Множество может быть задано перечислением или описанием. Задание множества перечислением заключается в составлении полного списка всех входящих в это множество элементов, заключенных в фигурные скобки. Например, множества N ={1;2;3;...}, Z ={0;±1;±2;...} − это заданные перечислением множества натуральных и целых чисел соответственно. Задание множества описанием состоит в записи всех свойств его элементов, заключенных в фигурные скобки. Например, множества Q = {х = p/q; p ∈Z; q ∈ N}, I ={x∈ R; x − числа с бесконечной непериодической дробной частью}} –это множества рациональных и иррациональных чисел соответственно, заданные описательно.

Множество называется конечным, если число его элементов конечно. Множество называют бесконечным, если число его элементов бесконечно. Множество называется счетным, если число его элементов бесконечно, но между ними и элементами множества N можно установить взаимно-однозначное соответствие. В противном случае бесконечное множество называется несчетным. Счетными множествами являются, например, числовые множества Z и Q , а несчетными – любой интервал или объединение интервалов и множество R . Упорядоченное множество – множество, каждому элементу которого можно присвоить номер.

Числовая ось – это некоторая прямая, на которой выбраны точка О, как точка начала отсчета, положительное направление, обозначенное стрелкой, и числовые обозначения.

Для интервалов на числовой оси существуют следующие обозначения:

Пусть a<b. (a,b) – интервал для a<x<b. [a,b] – сегмент для a<=x<=b. (-∞, +∞) – числовая прямая. ∞ - никогда не имеет строгое ограничение, т. е. всегда с круглой скобкой.

2. Абсолютная величина действительного числа. Понятие окрестности точки.

Абсолютная величина или модуль числа x — неотрицательное число, определение которого зависит от типа числа x. Обозначается: │x│.

В случае вещественного абсолютная величина есть непрерывная кусочно-линейная функция, определённая следующим образом:

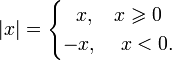
ξ – эпсилон – сколь угодно малое, фиксированное число. X будет принадлежать окрестностям точки х, если будет выполняться неравенство: │x-x0│<ξ

3. Понятие функции. Способы задания функции

Пусть x, y – непустые множества. xϵX, yϵY. Если к любому х из Х поставлено в соответствие одно определенное у, то будем считать, что задана функция, которую будем обозначать как y=f(x).

Способы задания функции:

А) Аналитический (в виде формулы)

Б) Графический (в виде графика)

В) Табличный (в виде таблицы значений)

Г) Описательный (например: если x>0, то y=x+1, если x<0, то y=x+30)

4. Свойства функции: четность и нечетность, монотонность, ограниченность, периодичность.

Если при замене x на –x значение функции не меняется, то эта уфункция называется четной. Если же наоборот – нечетной.

Монотонная функция — это функция, приращение которой не меняет знака, то есть либо всегда отрицательное, либо всегда положительное. Если в дополнение приращение не равно нулю, то функция называется строго монотонной. Монотонная функция — это функция, меняющаяся в одном и том же направлении. Функция возрастает, если большему значению аргумента соответствует большее значение функции. Функция убывает, если большему значению аргумента соответствует меньшее значение функции.

Функция f(x) называется ограниченной на данном промежутке (a,b), если существуют некоторые числа m и M такие, что m ≤ f(x) ≤ M при хє(a,b).

Периодическая функция ― функция, повторяющая свои значения через какой-то регулярный интервал, то есть не меняющая своего значения при добавлении к аргументу фиксированного ненулевого числа (периода функции).

Говоря более формально, функция периодична, если существует такое число T≠0 (период), что на всей области определения функции выполняется равенство  .

5. Показательная функция и ее свойства. Экспонента.

Периодическая функция ― функция, повторяющая свои значения через какой-то регулярный интервал, то есть не меняющая своего значения при добавлении к аргументу фиксированного ненулевого числа (периода функции).

Говоря более формально, функция периодична, если существует такое число T≠0 (период), что на всей области определения функции выполняется равенство  .

1. положительности: a^x > 0, x € R, а⁰ = I (a^x < 0 быть не может);

2. монотонности: x₁ < x₂ <=>

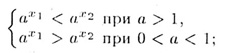
3. асимптотически стремится к нулю на бесконечности: a^x —> 0 при

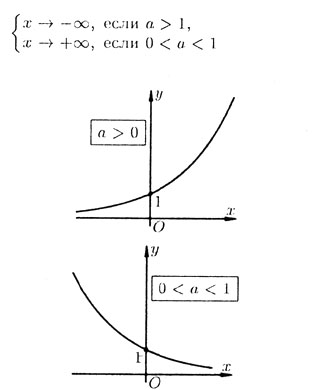
Прямая у = 0 называется горизонтальной асимптотой графика у = a^x.

Особо выделяется случай, когда в качестве основания степени выступает число e. Такая функция называется экспонентой(вещественной или комплексной).

7. Логарифмическая функция и ее свойства.

Функция  , ставящая в соответствие каждому положительному числу   его логарифм по данному положительному и отличному от единицы основанию  , называется логарифмической функцией.

А) Область определения х – x>0. yϵ(-∞, +∞).

Б) При   любая логарифмическая функция принимает значение, равное нулю

В) Если  , то функция   возрастающая (например,   и  ), т. е. большему положительному числу   соответствует больший логарифм (меньшему числу — меньший логарифм) и обратно: большему логарифму соответствует большее число (меньшему логарифму — меньшее число). При этом если  , то  , т. е. неограниченно убывает. Если   , то функция   убывающая (например,   и  ), т. е. большему положительному числу соответствует меньший логарифм и обратно: меньшему логарифму соответствует большее число. Если  , то  .

Г) Если   , то при   функция  , а при   функция  . 

7. Понятие обратной функции. Графики взаимообратных функций.

Обратная функция — функция, обращающая зависимость, выражаемую данной функцией.

Теорема. Строго монотонная функция обратима.

Теорема. Графики взаимно обратных функций в одной и той же координатной плоскости симметричны относительно биссектрисы первой и третьей четверти.

7. Понятие элементарной функции. Классификация элементарных функций.

Элементарные функции — функции, которые можно получить с помощью конечного числа арифметических действий и композиций из следующих основных элементарных функций:

• алгебраические:

  • степенная;

  • рациональная.

• трансцендентные:

  • показательная и логарифмическая;

  • тригонометрические и обратные тригонометрические.

Каждую элементарную функцию можно задать формулой, то есть набором конечного числа символов, соответствующих используемым операциям. Все элементарные функции непрерывны на своей области определения.

7. Предел числовой последовательности.

Числовая последовательность — это последовательность элементов числового пространства. Числовые последовательности являются одним из основных объектов рассмотрения в математическом анализе.

Определение. Пусть каждому натуральному числу n поставлено в соответствие некоторое единственное действительное число  (при этом разным натуральным числам n могут соответствовать и одинаковые действительные числа). В этом случае на множестве натуральных чисел определена функция:  , которая называется числовой последовательностью или просто последовательностью.

Последовательность обозначается:  , n=1, 2,… или  .

Числа  ,  ,… называются членами последовательности или ее элементами,  – общим членом последовательности, n – номером члена  .

По определению любая последовательность содержит бесконечное множество элементов.

Рассмотрим числовую последовательность, общий член которой приближается к некоторому числу  a  при увеличении порядкового номера  n. В этом случае говорят, что числовая последовательность имеет предел. 

Это означает, что  a  есть предел числовой последовательности, если её общий член неограниченно приближается к  a  при возрастании  n. Последовательность, имеющая предел, называется сходящейся; в противном случае – расходящейся.

Возрастающая или убывающая последовательность называется монотонной. По Теореме Вейерштрасса всякая монотонная и ограниченная последовательность имеет предел.

7. Определение числового предела в точке. Определение числового предела при x->∞

Все основывается на определении односторонних пределов. Без вычисления односторонних пределов не обойтись при нахождении вертикальных асимптот графика функции.

Определение (нахождение предела функции слева).

Число В называется пределом функции f(x) слева при  , если для любой сходящейся к а последовательности аргументов функции  , значения которых остаются меньше а ( ), последовательность значений этой функции сходится к В.

Обозначается  .

Определение (нахождение предела функции справа).

Число В называется пределом функции f(x) справа при  , если для любой сходящейся к а последовательности аргументов функции  , значения которых остаются больше а ( ), последовательность значений этой функции сходится к В.

Обозначается  .

Определение (существование предела функции в точке).

Предел функции f(x) в точке а существует, если существуют пределы слева и справа а и они равны между собой.

Замечание. Предел функции f(x) в точке а бесконечен, если пределы слева и справа а бесконечны.

Число А называется пределом функции f(x) при  , если для любой бесконечно большой последовательности аргументов функции (бесконечно большой положительной или отрицательной), последовательность значений этой функции сходится к А.

Обозначается  .