Хід роботи

1. Повторення раніше вивченого.

1. Які рівняння називають диференційними?

2. Які види розв’язків має диф.рівняння ?

3. Як розв’язуються диференціальні рівняння з відокремленими змінними?

2. Виконання індивідуального завдання.

Методичні рекомендації

Рівняння з відокремленими змінними

Якщо диференціальне рівняння першого порядку може бути представлене P (x) dx = Q (y) dy

де P (x) і Q (y) – функції лише однієї змінної.

Про інтегрувавши обидві частини, отримуємо загальний розв’язок (загальний інтеграл)

Однорідні диференціальні рівняння

Однорідним рівнянням називають рівняння у ^’= f(x,y) права частина якого f(x,y) є однорідною функцією нульового виміру відносно х та у. яка задовольняє умову f(tx, ty) = t^k f(x,y), де k – вимір або степінь однорідності.

Якщо k = 0, маємо функцію нульового виміру. Однорідну функцію нульового виміру завжди можна представити як функцію відношення змінних або ^. ( Це рівноцінно тому, що або ).

При його інтегруванні вводиться нова змінна або , що веде до рівняння з відокремленими змінними.

Приклад. Розв’язати диференціальне рівняння ( е^х + 2) у^’ = уе^х;

Розв’язання. Враховуючи, що у^' = , можна відокремити змінні в рівнянні

( е^х + 2) = уе^х;

Інтегруючи обидві частини, матимемо

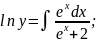
звідси, у = с(е^х +2) – загальним розв’язок заданого ДР.

Приклад. Розв’язати диференціальне рівняння (1+у²)dх-хуdу=0

Розведемо змінні в рівнянні (1+у²)dх = хуdу

проінтегруємо кожну частину

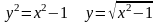
Приклад. Розв’язати рівняння ху = х + у.

Розв’язання. Поділимо обидві частини рівняння на х, маємо . Перевіримо функцію на однорідність f(x,y) = ; f(tx, ty) =1 отже права частина рівняння однорідна функція нульового виміру. Введемо нову змінну , тоді у = ux; . Підставляючи це у вихідне рівняння, отримаємо

.

Отже . Тоді загальний розв’язок рівний .

Практична робота по темі:

Диференціальні рівняння вищих порядків

Практична робота по темі:

Лінійні диференціальні рівняння вищих порядків зі сталими коефіцієнтами