
- •Визначники. Дії над матрицями
- •Хід роботи
- •Методичні рекомендації
- •Розв’язання системи лінійних рівнянь
- •Хід роботи
- •Методичні рекомендації
- •Дії над комплексними числами.
- •Хід роботи
- •Методичні рекомендації
- •Визначення елементів піраміди за допомогою координат вершин.
- •Хід роботи
- •Методичні рекомендації
- •Хід роботи
- •Методичні рекомендації
- •Хід роботи
- •Методичні рекомендації
- •Хід роботи
- •Методичні рекомендації
- •Хід роботи
- •Методичні рекомендації Правила диференціювання
- •Хід роботи
- •Методичні рекомендації Загальна схема дослідження функції. Побудова графіків
- •Хід роботи
- •Методичні рекомендації
- •Хід роботи
- •Методичні рекомендації
- •Хід роботи
- •Методичні рекомендації
- •Хід роботи
- •Методичні рекомендації
Хід роботи
Повторення раніше вивченого.
Яку дію називають інтегруванням?
Як розкласти правильний дріб на доданки ?
Яка схема інтегрування раціональних функцій?
Виконання індивідуального завдання.
Методичні рекомендації
1)
 2)
2)
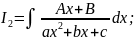
3)
 4)
4)

1. В інтегралі

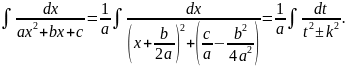
2. Інтеграл виду


Отже

3. Інтеграл виду
 виділенням повного квадрату підкореневого
виразу зводиться до видів:
виділенням повного квадрату підкореневого
виразу зводиться до видів:
 при а >0, або
при а >0, або
 при а < 0, які розглядались як
табличні («довгий» логарифм, або
арксинус).
при а < 0, які розглядались як
табличні («довгий» логарифм, або
арксинус).
4. Інтеграл виду

 зводиться до суми двох
зводиться до суми двох


Перший інтеграл типу
 а другий є не що інше як
а другий є не що інше як
 ( не враховуючи сталих коефіцієнтів що
є перед інтегралами)
( не враховуючи сталих коефіцієнтів що
є перед інтегралами)
Приклад. Знайти інтеграл
 .
.
Розв’язання. Враховуючи, що

Послідовно дістаємо:
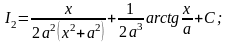

Приклад. Знайти інтеграл

Розв’язання. Простими перетвореннями зробимо в чисельнику похідну знаменника і розіб’ємо інтеграл на суму двох інтегралів.


Практична робота по темі:
Застосування інтегралів.
Мета: студенти повинні навчитись обчислювати визначені інтеграли.
Студенти повинні знати: таблицю інтегралів та методи інтегрування, формулу Ньютона-Лейбниця.
Студенти повинні вміти: використовувати визначний інтеграл для розв’язування різноманітних задач.
Література: Л – 1, стор. 362 – 411, Л – 6, стор. 355 – 410 .
Л – 10, стор.140 – 166, Л – 2, стор. 161– 175 .
Хід роботи
Повторення раніше вивченого.
Дайте означення визначеного інтеграла?
Перерахуйте основні властивості визначеного інтеграла .
В чому полягає геометричний зміст визначеного інтегралу ?
Виконання індивідуального завдання.
Методичні рекомендації
Якщо на відрізку
 функція
функція
 ,
то як відомо, площа криволінійної
трапеції обмеженою кривою
,
то як відомо, площа криволінійної
трапеції обмеженою кривою
 ,
віссю
,
віссю
 та прямими
та прямими
 ,
рівна
,
рівна
 .
.
Якщо ж
 на
,
то визначений інтеграл
на
,
то визначений інтеграл
 .
За абсолютною величиною він рівний
площі
.
За абсолютною величиною він рівний
площі
 відповідної криволінійної трапеції
відповідної криволінійної трапеції
Якщо потрібно обчислити площу, обмежену
кривими
 і прямими
,
за умови, що
і прямими
,
за умови, що
 ,
то досить обчислити інтеграл
,
то досить обчислити інтеграл
 .
.
Приклад 1. Знайти площу, обмежену
кривими
 .
.

Розв’язання. Знаходимо точки перетину кривих прирівнюючи функції

Отже враховуючи (7), маємо
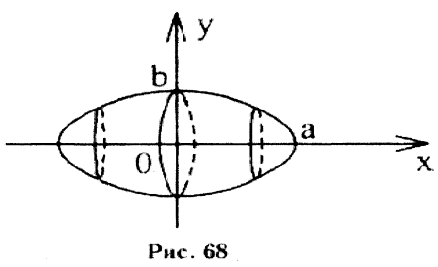
 Приклад 2. Знайти
об’єм тіла обертання, утвореного
обертанням еліпса
Приклад 2. Знайти
об’єм тіла обертання, утвореного
обертанням еліпса
 навколо осі.OX
навколо осі.OX
Р
Знайдемо
|
Враховуючи (7) об’єм тіла обертання рівний
 Приклад
3. Знайти довжину
кардіоїди
Приклад
3. Знайти довжину
кардіоїди
 .
.
Р озв’язання.
Спочатку побудуємо кардіоїду, надаючи
озв’язання.
Спочатку побудуємо кардіоїду, надаючи
значення кута
 .
.
|
Знайдемо
отримаємо половину шуканої довжини Отже, маємо
|
Практична робота по темі:
Диференціальні рівняння з відокремленими змінними
Мета: студенти повинні навчитись обчислювати диференціальні рівняння з відокремленими змінними
Студенти повинні знати: означення диференційних рівнянь, методи розв’язання таких рівнянь, таблицю інтегралів..
Студенти повинні вміти: розв’язувати рівняння І – го порядку, диференціальні рівняння з відокремленими змінними, однорідні диференційні рівняння.
Література: Л – 1, стор. 421 - 3455 Л – 6, стор. 426 -435 ,
Л – 10, стор.174 -177, Л – 2, стор. 181 – 190 .

 озв’язання.
Шуканий об’єм рівний
озв’язання.
Шуканий об’єм рівний
 .
. з рівняння еліпса
з рівняння еліпса .
.
 .
Змінюючи
від 0 до
.
Змінюючи
від 0 до
 ,
,
