Хід роботи

1. Повторення раніше вивченого.

1. Що називають задачами лінійного програмування?

2. В чому полягає графічний метод відшукання розв’язків задач лінійного програмування?

3. Яка двоїстість у задачах лінійного програмування?

2. Виконання індивідуального завдання.

Методичні рекомендації

На основі геометричної інтерпретації задач лінійного програмування розроблено графічний метод відшукання оптимальних значень функції. Використовують його для обмеженого класу задач із двома змінними, оскільки для чотирьох і більше змінних побудувати рисунок неможливо (а для трьох він не є наочним). Розв’язок шукаємо у такій послідовності:

1. Будуємо багатокутник розв’язків. Він утворюється внаслідок перетину окремих півплощин розв’язків З урахуванням обмежень х₁ ≥ 0,х₂ ≥ 0 багатокутник розв’язків завжди міститься у першому квадраті.

2. Знаходимо оптимальну точку. Вона за теоремою буде міститься у вершині багатокутника розв’язків. Лінії рівня, що проходять через оптимальні вершини багатокутника розв’язків, називають оптимальними (опорними). За допомогою вектора N можна на одному рисунку одночасно знайти max і min, тобто розв’язати відразу дві екстремальні задачі при одній і тій самій системі обмежень.

3. Обчислюємо оптимальні значення. Для цього знаходимо координати вершин max і min як загальний розв’язок рівнянь відповідних граничних прямих, що перетинаються в оптимальних вершинах. Знайдені координати підставляємо у Z й обчислюємо z_max та z_min.

Наприклад :Знайти найбільше і найменше значення функ­ції

z = -3 + 2х₁ + х₂ за таких обмежень:

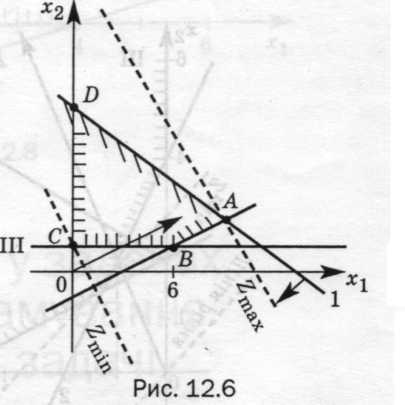Будуємо багатокутник розв'язків.

Для відшукання оптимальної точки будуємо вектор нормалі Початок цього вектора знаходиться в точці (0,0), а кінець - у точці (2,1). Рухаючись по лініях рівня в напрямку переконуємося, що z_max міститься в точці А, z_max – у точці С.

3 . Обчислюємо оптимальні значення. Точка А є перетином граничних прямих І і II:

X₁+ X₂ =7

2X₁ + 3X₂ = - 4

Із рисунка випливає, що Х₁ = 5, Х₂ = 2, А = (5,2), a

z_max = 2· 5+1·2-3= 9.

Точка В (0,1) є перетином граничних прямих III та IV:

Х₂ = 1, Х₁ = 0.

Отже, z_min = 2· 0 + 1·1-3 = -2.

Практична робота по темі:

Транспортні задачі .

Мета: студенти повинні навчитись розв’язувати транспортні задачі з правильним і неправильним балансом

Студенти повинні знати: галузі застосування транспортних задач, різницю між задачами з правильним і неправильним балансом

Студенти повинні вміти: розв’язувати транспортні задачі

Література: Л – 11, стор. 436 – 445 .

Хід роботи

1. Повторення раніше вивченого.

1. В чому полягає постановка транспортної задачі?

2. Які існують методи розв’язання транспортної задачі?

3. Як розв’язують задачі з неправильним балансом?

2. Виконання індивідуального завдання.

Методичні рекомендації

Оскільки транспортна задача є задачею лінійного програмування, її можна розв’язати багатьма способами. Виберемо найпростіший метод осереднених коефіцієнтів. За цим методом обчислюємо середні вартості в рядках і стовпцях матриці перевезення:

С_Аi = ; C_{Bj =}

Після цього знаходимо усереднені коефіцієнти k_ij за формулою k_ij = c_ij – (c_Ai + c_Bj).

Пункт відправ­лення	Пункт споживання						Запас
	В1	В2	В3	В4	В5
А1						60
А2						35
А3						40
Потреба	22	45	20	18	30	135

Потім заповнюємо послідовно клітинки з найменшими значеннями коефіцієнтів к_іj. Сума чисел по рядку відповідає кількості запасів, сума чисел по стовпчику відповідає потребам.

Практична робота по темі:

Обчислення границі функції.

Мета: студенти повинні навчитись обчислювати границі різноманітних функцій, користуватися першою та другою визначною границею

Студенти повинні знати:методи . обчислення границі різноманітних функцій, першу і другу визначну границю.

Студенти повинні вміти: використовувати методи . обчислення границі різноманітних функцій, першу і другу визначну границю.

Література: Л – 1, стор. 149 – 175 ., Л – 2, стор. 74 – 81

Л – 6, стор. 161 - 177 , Л – 10, стор.46 – 61,