21. Необходимые признаки сходимости ряда.

Если числовой ряд сходится, то общий член этого ряда стремится к нулю при неограниченном возрастании n (номер члена ряда): =0.

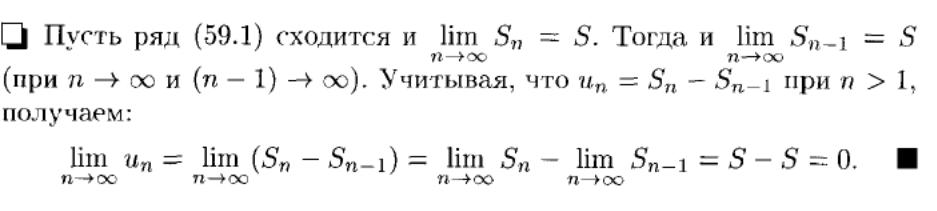
22. Признак сравнения.

а) в форме неравенства:

Пусть даны два ряда с положительными числами: (60.1), (60.2); U_n>0; V_n>0 и пусть последний член ряда (1) не превышает соответствующий член ряда (2), т.е. U_n ≤ V_n (3), тогда если:

1.Ряд (2) сходится, то сходится и ряд (1).

2.Если ряд (1) расходится, то расходится и ряд (2).

Доказательство:

б) в предельной форме:

Определение: Если предел отношения n-ных членов, т.е. , то ряды (1) и (2) ведут себя относительно сходимости одинаково.

Доказательство

23. Признак Даламбера для рядов с неотрицательными членами.

Если существует предел , то ряд сходится, если 0<L<1, расходится, если L>1.

Замечания: 1. Если L= 1, то ряд может быть как сходящимся, так и расходящимся.

2. Признак Деламбера целесообразно применять, когда общий член ряда содержит выражение вида n! или aⁿ.

24. Признак Коши для рядов с неотрицательными членами.

Если существует и конечен предел: , то ряд сходится, если L<1, и расходится, если L>1; если L=1, то вопрос о сходимости результата не даст.

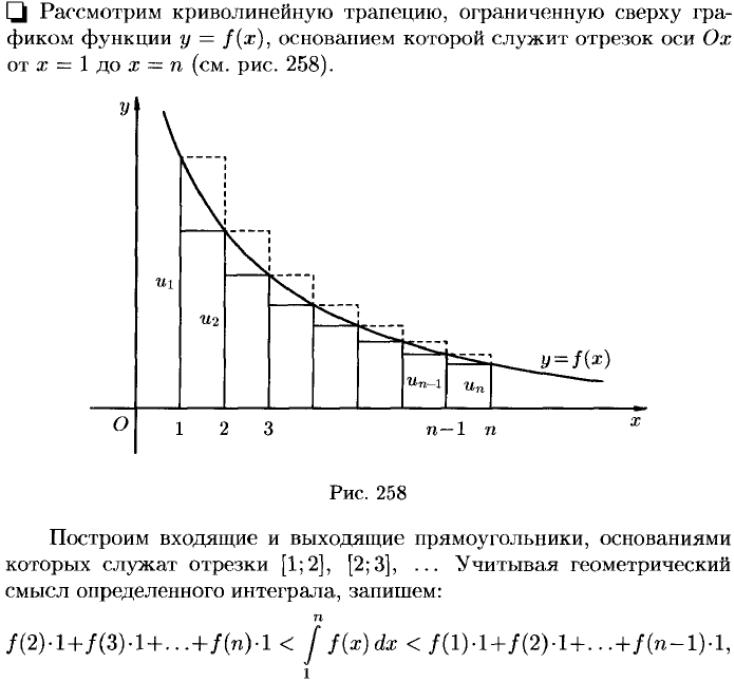
25. Интегральный признак Коши.

Рассмотрим знакоположительный ряд

. Если функция _φ(k), где k – непрерывная переменная, непрерывная, положительная и убывающая на полуинтервале [1;+∞], то ряд φ₍₁₎+φ₍₂₎+…+φ_(n)+…+ и собственный интеграл ведут себя одинаково относительно сходимости.

26. Числовые ряды с произвольными членами. Теорема Лейбница для знакочередующих­ся рядов. Оценка остатка ряда.

Знакочередующимся называется ряд ,если:

Числовой ряд называется абсолютно сходящимся, если сходится ряд, составленный из модулей его членов .

Признак Лейбница это достаточный признак сходимости

Знакочередующийся ряд сходится, если :1) его члены убывают по абсолютной величине и 2) его абсолютная величина общего члена стремится к нулю, когда n→∞, т.е. .

При этом S ряда удовлетворяет неравенствам: 0< S< U₁

Интегральный признак Коши позволяет оценить остаток r_n знакоположительного ряда. Из полученного в доказательстве выражения с помощью несложных преобразований получаем: .

Доказательство:

27. Необходимое и достаточное условие сходимости рядов с комплексными членами.

Ряд с комплексными членами сходится тогда, и только тогда, когда сходятся ряды, составленные из действительных и мнимых частей членов ряда.

Если расходится хоть один составленный ряд, то и весь ряд расходится.

Ряд с комплексными членами сходится абсолютно, если сходится ряд, составленный из модулей комплексных чисел.

- модуль комплексного числа

28. Абсолютная и условная сходимость. Свойства абсолютно сходящихся рядов (б/д). Признаки Даламбера и Коши для рядов с произвольными членами

Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд . Если ряд из модулей расходится, а сам ряд сходится, то его называют условно сходящимся.

Свойства:

1) Для абсолютной сходимости ряда необходимо и достаточно, чтобы его можно было представить в виде разности двух сходящихся рядов с неотрицательными членами.

2) В сходящемся ряде любая группировка членов ряда, не изменяющая их порядка, сохраняет сходимость и величину ряда.

3) Если ряд сходится абсолютно, то ряд, полученный из него любой перестановкой членов, также абсолютно сходится и имеет ту же сумму.

4)При любой группировке членов абсолютно сходящегося ряда (при этом число групп может быть как конечным, так и бесконечным и число членов в группе может быть как конечным, так и бесконечным) получается сходящийся ряд, сумма которого равна сумме исходного ряда.

5) Если ряды и сходятся абсолютно и их суммы равны соответственно S и s, то ряд, составленный из всех произведений вида u_iυ_k, i,k = 1,2,… взятых в каком угодно порядке, также сходится абсолютно и его сумма равна S×s - произведению сумм перемножаемых рядов.

Признаки Даламбера и Коши для рядов с произвольными членами.

Пусть ряд ∑u_n имеет члены произвольных знаков.

Признак Даламбера: Если существует предел _, то при р<1 ряд ∑u_n абсолютно сходится, при p>1 ряд расходится.

Признак Коши: Если существует _, то при р<1 ряд ∑u_n абсолютно сходится, при p>1 ряд расходится.