1. Растяжение и сжатие. Напряжения и перемещения. Условие прочности.

Осевое (центральное) растяжение или сжатие прямого бруса вызывается внешними силами, вектор равнодействующей которых совпадает с осью бруса.

В этом случае все внутренние силовые факторы в поперечных сечениях бруса, кроме растягивающей или сжимающей силы, равны 0. Растягивающие продольные силы принято считать положительными, а сжимающие – отрицательными. Продольная сила в некоторых сечениях равна алгебраической сумме проекций на ось стержня всех внешних сил, расположенных по одну сторону от рассматриваемого сечения.

Напряжения, существующие в теле, связаны определенными зависимостями с упругими деформациями. Рассуждая формально, можно было бы описать деформированное состояние тела только, через компоненты деформаций, не прибегая к напряжениям. Однако оценка состояния тела через напряжения оказывается удобной, особенно если рассматриваются вопросы, связанные с прочностью.

Суммирование деформаций приводит к образованию перемещений. Если обозначить перемещения соответственно осям X, Y, Z буквами и, v, w, то наблюдаемые деформации можно выразить через перемещения следующим образом:

; ; .

Условие прочности:

δ=P/A<=[δ].

2. Основные понятия в сопротивлении материалов. Определения и допущения. Внешние и внутренние силы. Метод сечений.

Сопротивление материалов – наука о прочности, жесткости и надежности элементов инженерных конструкций. Методами сопротивления материалов ведутся практические расчеты и определяются необходимые размеры деталей машин, различных конструкций и сооружений. Основные понятия сопротивления материалов опираются на законы и теоремы общей механики и в первую очередь на законы статики.

Сопротивление материалов рассматривает задачи, где наиболее существенными являются свойства деформируемых тел. Сопротивление материалов имеет целью создать практически приемлемые простые приемы расчета типичных, наиболее часто встречающихся элементов конструкций.

Введем основные понятия, принимаемые при изучении дисциплины.

Прочность – это способность конструкции выдерживать заданную нагрузку, не разрушаясь.

Жесткость – способность конструкции к деформированию в соответствие с заданным нормативным регламентом.

Деформирование – свойство конструкции изменять свои геометрические размеры и форму под действием внешних сил

Устойчивость – свойство конструкции сохранять при действии внешних сил заданную форму равновесия.

Силы – мера механического взаимодействия тел. Если конструкция рассматривается изолировано от окружающих тел, то действие последних заменяют силами, которые называют внешними. К ним относят активные силы, для восприятия которых создана конструкция, и реактивные (реакции связей). Внешние силы по способу приложения могут быть сосредоточенными и распределёнными. Внутренние силы – дополнительные силы взаимодействия между частицами тела, возникающими вследствие его деформации. Внутренние силы определяются с помощью метода сечений.

3. Закон Гука. Модуль упругости. Диаграмма растяжения. Механические характеристики материалов.

Гука закон - основной закон, выражающий связь между напряжённым состоянием и деформацией упругого тела. Установлен английским физиком Р. Гуком в 1660 для простейшего случая растяжения или сжатия стержня.

Обобщённый закон Гука — для тела произвольной формы — утверждает, что 6 величин, определяющих напряжённое состояние в точке, выражаются линейно через 6 величин, определяющих деформацию в окрестности рассматриваемой точки. Коэффициент пропорциональности в этих соотношениях называются модулями упругости.

Закон: .

Модуль упругости - величина, характеризующая упругие свойства материалов при малых деформациях. Модуль сдвига G, модуль продольной упругости Е и коэффициент Пуассона материала связаны зависимостью

.

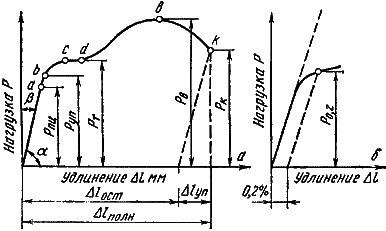
Где P_пц – предел пропорциональности,

P_уп – предел прочности,

P_т – текучести.

Под механическими характеристиками подразумеваются значения напряжений и деформаций, соответствующие определенным точкам на диаграмме условных напряжений.

Пределом пропорциональности называется наибольшее напряжение, до которого деформации прямо пропорциональны напряжениям. Пределом упругости называется напряжение, до которого материал не получает остаточных деформаций. Пределом текучести называется напряжение, при котором деформации растут без заметного увеличения нагрузки. Пределом прочности, или временным сопротивлением, называется максимальное напряжение, выдерживаемое материалом при растяжении.