29.Уравнение Бернулли

Определение. Уравнением Бернулли называется уравнение вида

,

где и - непрерывные функции (в частности – постоянные), а .

Метод Бернулли. Решение уравнения Бернулли ищем в виде произведения функций . Функцию находим из уравнения , а - из уравнения .

Метод Лагранжа (метод вариации постоянной). После интегрирования уравнения , ищем решение уравнения Бернулли в виде , где функция находится из уравнения .

Приведение к линейному уравнению. С помощью подстановки уравнение Бернулли сводится к линейному уравнению относительно функции

.

30. Уравнение Риккати

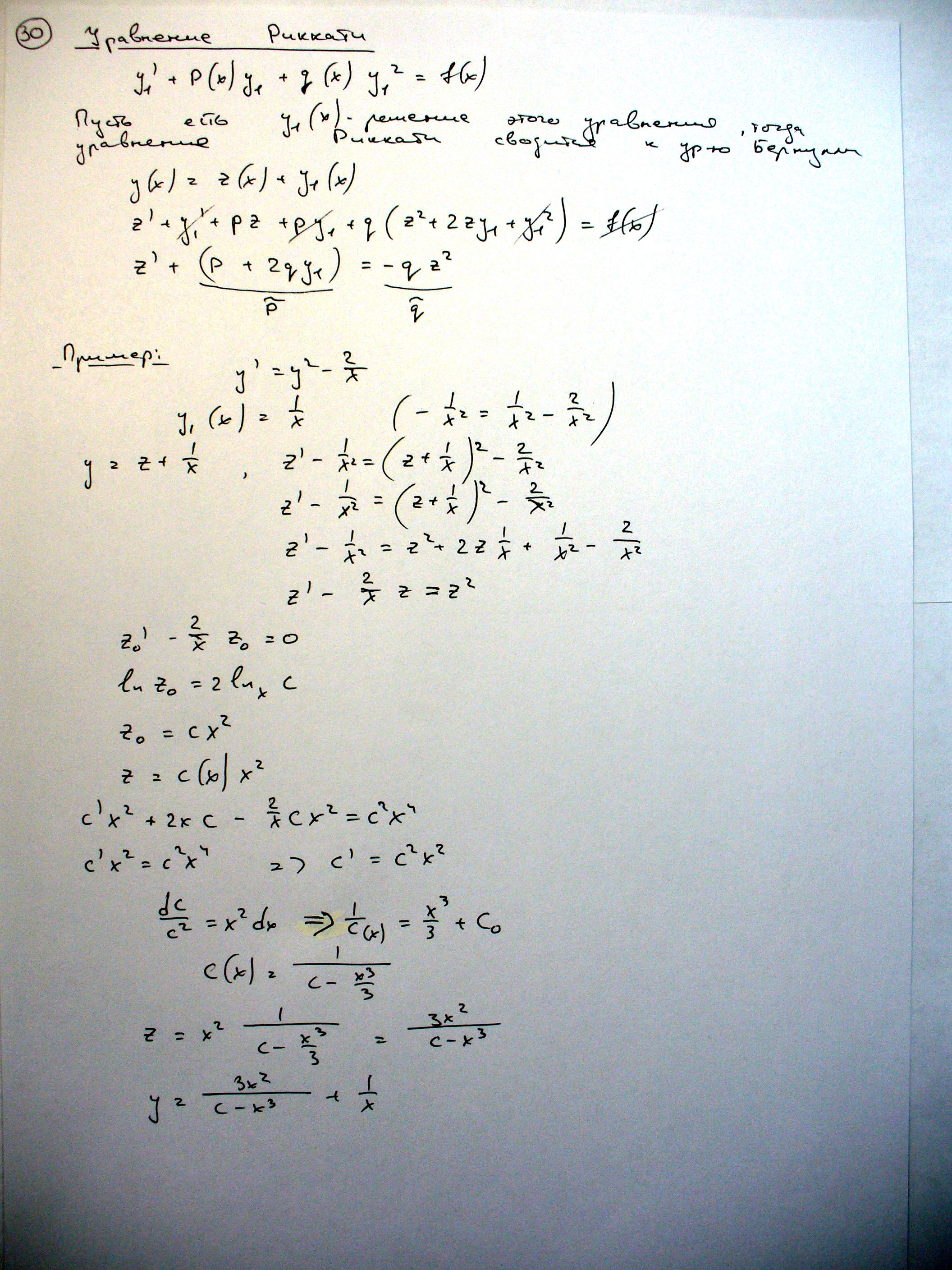
31. Уравнения в полных дифференциалах. Интегрирующий множитель.

I. Уравнение в полных дифференциалах.

Определение. Дифференциальное уравнение

(1)

называется уравнением в полных дифференциалах, если его левая часть есть полный дифференциал некоторой функции , т.е.

.

Так как , общий интеграл уравнения (1) имеет вид

.

Для того, чтобы уравнение (1) было уравнением в полных дифференциалах, необходимо и достаточно, чтобы выполнялось условие

. (2)

Функция может быть найдена из системы дифференциальных уравнений

либо с помощью вычисления интегралов по формуле

,

где - некоторая фиксированная точка из области непрерывности функций и их частных производных.

II. Интегрирующий множитель.

Если условие (2) не выполняется для уравнения (1), то в ряде случаев его можно свести к уравнению в полных дифференциалах умножением на некоторую функцию ( ), называемую «интегрирующим множителем». При правильном нахождении интегрирующего множителя должно выполняться соотношение

.

В общем случае нахождение интегрирующего множителя весьма затруднительно. Выделяют два важных случая.

1. Пусть отношение зависит только от переменной , тогда интегрирующий множитель можно найти с помощью формулы

.

2. Если же отношение зависит только от переменной , то справедлива формула

.

32.Огибающие семейства кривых, особые решение и особые точки (узел, седло, центр, фокус)

33. Дифференциальные уравнения второго порядка.

Определение. Уравнение

, (1)

связывающее между собой независимую переменную , неизвестную функцию и первые ее две производные, называется дифференциальным уравнением второго порядка. Если уравнение (1) можно записать в виде , то говорят, что оно разрешимо относительно второй производной.

Функция , зависящая от двух произвольных постоянных , и обращающая уравнение (1) в тождество при подстановке ее в это уравнение вместе со своими производными, называется его общим решением. Задача Коши для уравнения второго порядка формулируется следующим образом: найти решение уравнения (1), удовлетворяющее заданным начальным условиям , где - некоторые числа. Для сформулированной задачи Коши, имеет место теорема существования и единственности решения, аналогичная теореме для уравнений первого порядка.

Теорема. Если функция и ее частные производные непрерывны в некоторой области , содержащей точку с координатами , то существует и притом единственное решение уравнения (1), удовлетворяющее начальным условиям .

Задача Коши состоит в нахождении интегральной кривой , проходящей через точку и имеющей заданный угловой коэффициент (заданное направление) касательной к этой кривой в этой точке, т.е. .

34.Уравнения вида .

Решения уравнений этого вида находятся непосредственным интегрированием

и, далее,

.

35. Уравнения вида .

Уравнения такого вида допускают понижение порядка с помощью подстановки . Учитывая, что , получаем уравнение первого порядка

,

решая которое находим функцию . Окончательное решение рассматриваемого уравнения второго порядка находится интегрированием уравнения .

Замечание. Аналогичной подстановкой понижается порядок уравнения .

36. Уравнения вида .

Такие уравнения допускают понижение порядка подстановкой . Следовательно, . Получающееся уравнение первого порядка имеет вид

.

Окончательное решение рассматриваемого уравнения второго порядка находится интегрированием уравнения .

Замечание. Аналогичной подстановкой понижается порядок уравнения .

37.Линейные дифференциальные уравнения второго порядка (определение, общее решение)

Определение. Линейным однородным дифференциальным уравнением второго порядка называется уравнение

, (1)

где - функции, непрерывные на некотором интервале . Справедлива теорема. Если функции и являются частными решениями уравнения (1), то решением этого уравнения является также функция , где и - произвольные постоянные.

Функции и называются линейно независимыми на интервале , если равенство , где , выполняется тогда и только тогда, когда . В противном случае они называются линейно зависимыми. Для линейной зависимости необходимо и достаточно, чтобы для всех выполнялось равенство , т.е. функции и должны быть пропорциональны.

Определитель

называется определителем Вронского или вронскианом.

Теорема. Если дифференцируемые функции и линейно зависимы на интервале , то определитель Вронского на этом интервале тождественно равен нулю.

Теорема. Если функции и - линейно независимые решения уравнения (1) на интервале , то определитель Вронского на этом интервале нигде не обращается в нуль.

Совокупность любых двух линейно независимых на интервале частных решений уравнения (1) определяет фундаментальную систему решений этого уравнения.

Теорема. Если два частных решения и уравнения (1) образуют на интервале фундаментальную систему, то общим решением этого уравнения является функция , где и - произвольные постоянные.

Если в уравнении (1) и - постоянные величины, то такое уравнение

(2)

называется линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами.