33. Составление уравнений колебаний методом урав-нений Лагранжа 2-го рода

В большинстве задач деформируемое состояние системы определяется n обобщенными координатами q1,…qn - кинетическую энергию масс T и потенциальную сил упругости U можно представить в виде зависимостей:

T=T(q1,…,qn); U=U(q1,…,qn)

Б удем считать, что внешние силы P таковы, что работа их пропорционально вариациям перемещений:

Тогда Ji-инерционные силы и Si-упругие силы можно записать как:

(1)

(1)

Запишем условие равновесия с помощью возможных перемещений:

П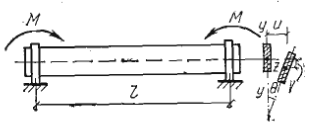 одставим в это уравнение равенства (1):

-уравнение движение Лагранжа (2).

(пунктир продолжить и обозначить перемещения по вертикали и горизонтали)

Для такой системы кинетическая энергия массы m:

q1 и q2- перемещения

Потенциальная энергия деформации стержней:

Возможная работа силы P на перемещениях δq1 и δq2:



Находим производные для i=1:

Аналогично находим производные для i=2

Подставляем в (2),получаем:

34. Устойчивость плоской формы изгиба

При большой разнице между моментами инерции изгибаемой балки, когда неустойчивой становится плоская форма изгиба.

Рассмотрим устойчивости балки с постоянным прямоугольным сечением по длине при чистом изгибе.

Балка опирается на идеальные шарниры - позволяют поворачиваться в плоскости изгиба; на опорах установлены устройства, позволяющие свободно поворачиваться балке относительно другой оси, но при этом сечения опорные не поворачиваются относительно продольной оси самой балки.

В деформированном состоянии произвольное сечение m-m сместится по вертикали и горизонтали v и u, а также повернется на угол Ɵ

EIz и EIy – изгибная жесткость относительно осей z и y соответ.

GId – жесткость при кручении:

- ф-ла Тимошенко.

ДУ для изгиба в 2-х плоскостях при кручении в упругой стадии:

(1)

(2)

(3)

u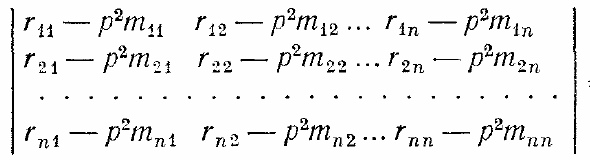 и Ɵ содержаться в 2-х последних уравн., рассмотрим их, 1 раз дифференцируем (3)

Из этого выражения находим подставляем в (2):

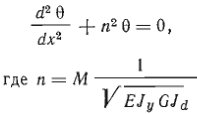
Решение уравнения:

Ищем const A и B, гранич. Усл.:

X=0, Ɵ=0 A=0, Bsin(nl)=0

B=0 соответствует изгибу без потери устойчивости. Примем sin(nl)=0, что возможно при nl=π, 2π, 3π…

Практическое значение из бесконечного числа корней имеет наименьший nl= π, ему соответствует критический момент:

- критический момент потери устойчивости плоской формы изгиба полосы.

35.Собственные частоты и формы колебаний

Частота свободных колебаний системы называется собственной.

П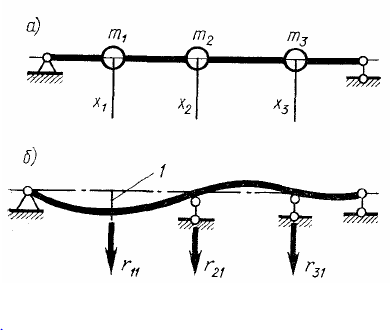 ри свободном колебании возмущающие силы отсутствуют и уравнение движения является однородным:

(1)

Решение системы:

(i=1,2…n)

p- угловая частота; ui- const;

φ- фаза колебаний.

Подставим xi (1) и сократим на sin(pt+ φ):

(i=1,2…n). Это система уравнений однородных линейных относительно ui.Эта система имеет решения только при определителе равном нулю:

Δр²=

= 0 – частотное (вековое) уравнение. Если положение системы, от которого отсчитывается перемещения xi, является положением устойчивого статического равновесия, то n корней уравнения действительны и положительны  система с n степенями свободы имеет n собственных частот. В общем случае все корни, а значит и частоты, различны.

Каждой собственной частоте pk соответствует опред. форма колебания, т.е. опред. соотношение между всеми амплитудными перемещениями ui.

Обычно формы и частоты собственных колебаний нумеруют от меньшего к большему: k=1-min, k=n-max.

К аждому k отвечает решение уравнения в виде:

-движение в соответ. с этим уравн. – главные колебания системы.

Т .к. уравн. движения-линейное, то линейная комбинация решений:

В это уравнение входит 2n const C1k и C2k (k=1,2…n)это общее решение системы (1).