
- •1. Законы Ньютона
- •2. Законы изменения и сохранения импульса механической системы.
- •3. Работа силы, мощность. Консервативные и неконсервативные силы.
- •4. Универсальная связь между потенциальной энергией и силой (градиент). Закон сохранения и изменения механической энергии.
- •6. Теорема Штейнера. Работа силы при вращении. Кинетическая энергия при вращательном и плоском движении тела.
- •7. Преобразования Галилея. Кинематика относительного движения. Абсолютное, относительное и переносное ускорение частиц. Силы инерции. Центробежная сила.
- •8. Механика жидкостей. Уравнение Бернулли.
- •9. Постулаты специальной теории относительности Эйнштейна. Преобразования Лоренца. Относительность пространства и времени.
- •10. Идеальный газ. Изопроцессы. Уравнение состояния идеального газа (уравнение Клапейрона–Менделеева).
- •12. Работа расширения. Первое начало термодинамики
- •13. Теплоемкость. Уравнение Майера. Адиабатический процесс. Уравнение Пуассона
- •14. Семейство политропных процессов. Теплоемкость газа в политропных процессах. Работа и теплота в политропных процессах
- •15. Закон распределения молекул по скоростям и кинетическим энергиям (распределение Максвелла).
- •16. Барометрическая формула. Закон распределения частиц во внешнем потенциальном поле (распределение Больцмана).
- •18. Прямой и обратный круговые процессы (циклы). Принцип действия теплового двигателя и холодильной машины. Цикл Карно. Термический кпд цикла Карно
- •19. Энтропия. Второе начало термодинамики. Основное уравнение термодинамики (термодинамическое тождество).
- •20. Термодинамическая вероятность состояния. Формула Больцман
- •21. Термодинамические потенциалы.
- •22. Вандерваальсовский газ. Уравнение Ван-дер-Ваальса.
- •23. Внутренняя энергия вандерваальсовского газа. Адиабатный дроссельный эффект Джоуля -Томсона.
- •24. Фазовые переходы первого рода. Уравнение Клапейрона - Клаузиуса для однокомпонентных систем. Простейшие диаграммы состояния (pT-диаграммы). Тройная точка. Критическая точка
- •25. Поверхностное натяжение. Смачивание жидкостей.
- •26. Избыточное давление над искривленной поверхностью жидкости. Капиллярные явления.
- •27. Полупроницаемые мембраны. Явление осмоса.
14. Семейство политропных процессов. Теплоемкость газа в политропных процессах. Работа и теплота в политропных процессах
Политропный процесс это процесс, в котором теплоемкость остается постоянной. Политропным процессом являются изохорный, изобарный, изотермический и адиабатный процессы, потому что все они имеют общую особенность - они происходят при постоянной теплоемкости.
В первых двух процессах теплоемкости соответственно равны Cv и Cp, в изотермическом процессе (dT=0) теплоемкость равна бесконечности, в адиабатном политропный процесс равна нулю. График политропного процесса показан ниже:
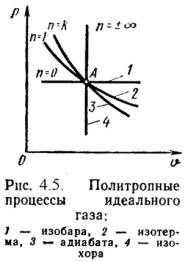
График политропного процесса
Политропа
Политропа это
график зависимости между параметрами
состояния идеального газа при ![]() .
Политропа в координатах p, V - гипербола,
занимающая промежуточное положение
между изотермой и адиабатой.
.
Политропа в координатах p, V - гипербола,
занимающая промежуточное положение
между изотермой и адиабатой.
Исходя из первого начала термодинамики при условии постоянства теплоемкости ( ), можно вывести уравнение политропы:
![]() - уравнение
политропы,
- уравнение
политропы,
где ![]() -
показатель политропы.
-
показатель политропы.
15. Закон распределения молекул по скоростям и кинетическим энергиям (распределение Максвелла).
Молекулы газа при своем движении постоянно сталкиваются. Скорость каждой молекулы при столкновении изменяется. Она может возрастать и убывать. Однако среднеквадратичная скорость остается неизменной. Это объясняется тем, что в газе, находящемся при определенной температуре, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям, которое подчиняется определенному статистическому закону. Скорость отдельной молекулы с течением времени может меняться, однако доля молекул со скоростями в некотором интервале скоростей остается неизменной.
Нельзя ставить вопрос: сколько молекул обладает определенной скоростью. Дело в том, что, хоть число молекул очень велико в любом даже малом объеме, но количество значений скорости сколь угодно велико (как чисел в последовательном ряде), и может случиться, что ни одна молекула не обладает заданной скоростью.
|
Основываясь
на опыте Штерна, можно ожидать, что
наибольшее число молекул будут иметь
какую-то среднюю скорость, а доля быстрых
и медленных молекул не очень велика.
Необходимые измерения показали, что
доля молекул
,
отнесенная к интервалу скорости Δv,
т.е. ![]() ,
имеет вид, показанный на рис. 3.3. Максвелл
в 1859 г. теоретически на основании теории
вероятности определил эту функцию. С
тех пор она называется функцией
распределения молекул по скоростям или
законом Максвелла.
,
имеет вид, показанный на рис. 3.3. Максвелл
в 1859 г. теоретически на основании теории
вероятности определил эту функцию. С
тех пор она называется функцией
распределения молекул по скоростям или
законом Максвелла.
Аналитически она выражается формулой
|
|
где m – масса молекулы, k – постоянная Больцмана.
Установление этой зависимости позволило определить кроме уже известной среднеквадратичной скорости еще две характерные скорости – среднюю и наиболее вероятную. Средняя скорость – это сумма скоростей всех молекул, деленная на общее число всех молекул в единице объема.
Средняя скорость, подсчитанная на основании закона Максвелла, выражается формулой
|
|
или
|
|
Наиболее вероятная скорость – это скорость, вблизи которой на единичный интервал скоростей приходится наибольшее число молекул. Она рассчитывается по формуле:
|
|
Сопоставляя все три скорости:
1) наиболее
вероятную  ,
,
2) среднюю  ,
,
3) среднюю
квадратичную  ,
– видим, что наименьшей из них является
наиболее вероятная, а наибольшей –
средняя квадратичная. Относительное
число быстрых и медленных молекул мало
(рис. 3.4).
,
– видим, что наименьшей из них является
наиболее вероятная, а наибольшей –
средняя квадратичная. Относительное
число быстрых и медленных молекул мало
(рис. 3.4).
|
|
Кривые распределения молекул по скоростям начинаются в начале координат, асимптотически приближаются к оси абсцисс при бесконечно больших скоростях. Слева от максимума кривые идут круче, чем справа. То, что кривая распределения начинается в начале координат, означает, что неподвижных молекул в газе нет. Из того, что кривая асимптотически приближается к оси абсцисс при бесконечно больших скоростях, следует, что молекул с очень большими скоростями мало. Это легко объяснимо. Для того чтобы молекула могла приобрести при столкновениях очень большую скорость, ей необходимо получить подряд много таких столкновений, при которых она получает энергию, и ни одного столкновения, при котором она ее теряет. А такая ситуация маловероятна.

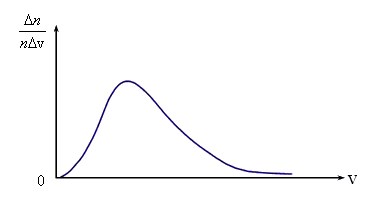 Рис.
3.3
Рис.
3.3 ,
, .
. .
. Рис.
3.4
Рис.
3.4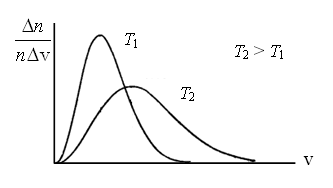 Рис.
3.5
Рис.
3.5