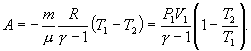- •1. Законы Ньютона
- •2. Законы изменения и сохранения импульса механической системы.
- •3. Работа силы, мощность. Консервативные и неконсервативные силы.
- •4. Универсальная связь между потенциальной энергией и силой (градиент). Закон сохранения и изменения механической энергии.
- •6. Теорема Штейнера. Работа силы при вращении. Кинетическая энергия при вращательном и плоском движении тела.
- •7. Преобразования Галилея. Кинематика относительного движения. Абсолютное, относительное и переносное ускорение частиц. Силы инерции. Центробежная сила.
- •8. Механика жидкостей. Уравнение Бернулли.
- •9. Постулаты специальной теории относительности Эйнштейна. Преобразования Лоренца. Относительность пространства и времени.
- •10. Идеальный газ. Изопроцессы. Уравнение состояния идеального газа (уравнение Клапейрона–Менделеева).
- •12. Работа расширения. Первое начало термодинамики
- •13. Теплоемкость. Уравнение Майера. Адиабатический процесс. Уравнение Пуассона
- •14. Семейство политропных процессов. Теплоемкость газа в политропных процессах. Работа и теплота в политропных процессах
- •15. Закон распределения молекул по скоростям и кинетическим энергиям (распределение Максвелла).
- •16. Барометрическая формула. Закон распределения частиц во внешнем потенциальном поле (распределение Больцмана).
- •18. Прямой и обратный круговые процессы (циклы). Принцип действия теплового двигателя и холодильной машины. Цикл Карно. Термический кпд цикла Карно
- •19. Энтропия. Второе начало термодинамики. Основное уравнение термодинамики (термодинамическое тождество).
- •20. Термодинамическая вероятность состояния. Формула Больцман
- •21. Термодинамические потенциалы.
- •22. Вандерваальсовский газ. Уравнение Ван-дер-Ваальса.
- •23. Внутренняя энергия вандерваальсовского газа. Адиабатный дроссельный эффект Джоуля -Томсона.
- •24. Фазовые переходы первого рода. Уравнение Клапейрона - Клаузиуса для однокомпонентных систем. Простейшие диаграммы состояния (pT-диаграммы). Тройная точка. Критическая точка
- •25. Поверхностное натяжение. Смачивание жидкостей.
- •26. Избыточное давление над искривленной поверхностью жидкости. Капиллярные явления.
- •27. Полупроницаемые мембраны. Явление осмоса.
12. Работа расширения. Первое начало термодинамики
Работа расширения |
Работа, производимая газом при расширении. Для бесконечно малого приращения объема dv она равна dW = pdv. Вся работа при
расширении от объема W, соответствующего
начальному состоянию, до объема v2,
соответствующего конечному состоянию,
выражается определенным интегралом |
Первый
закон термодинамики представляет собой
закон сохранения энергии. Если сообщить
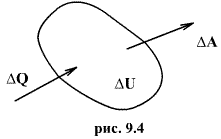
телу количество тепла ![]() (рис.9.4),
тело может за счет этого тепла увеличить
свою внутреннюю энергию на величину
(рис.9.4),
тело может за счет этого тепла увеличить
свою внутреннюю энергию на величину ![]() и,
кроме того, выполнить работу
и,
кроме того, выполнить работу ![]() ,
причем в силу закона сохранения
энергии: ΔQ=ΔU+ΔA
,
причем в силу закона сохранения
энергии: ΔQ=ΔU+ΔA
Последние выражение удобнее записать для малого изменения состояния системы, вызванного сообщением ей малого количества тепла δQ и совершением системой элементарной работы δA
δQ = dU+δA |
(9.10) |
Различие
в записи малого приращения внутренней
энергии dU и элементарного количества
теплоты δQ, а также элементарной
работы δA объясняется следующим
соображениями. Как уже отмечалось,
внутренняя энергия системы являеться
функцией ее состояния. Следоватено, при
любом процессе, в результате которого
система вновь возвратилась в некоторое
состояние, полное изменение ее внутренней
энергии равно нулю. Математически это
записываться в виде уравнения ![]() которое
являеться необходимым и достаточным
условием того, что внутренняя энергия
системы U представляет собой, так
называемыйполный дифференциал dU.
Работа и теплота такими свойствами не
обладают. Поэтому δQ и δА не
являються полными дифференциалами, эти
величины являються “Функциями процесса”
(см. рис. 9.3)
которое
являеться необходимым и достаточным
условием того, что внутренняя энергия
системы U представляет собой, так
называемыйполный дифференциал dU.
Работа и теплота такими свойствами не
обладают. Поэтому δQ и δА не
являються полными дифференциалами, эти
величины являються “Функциями процесса”
(см. рис. 9.3)
Таким образом:
δQ = dU+δA
Первый закон термодинамики формулируеться следующим образом: теплота, переданная системе, расходуеться на изменение ее внутренней энергии и на совершение работы.
13. Теплоемкость. Уравнение Майера. Адиабатический процесс. Уравнение Пуассона
Теплоёмкость тела характеризуется количеством теплоты, необходимой для нагревания этого тела на один градус:
|
|
|
(4.2.1) |
Размерность теплоемкости: [C] = Дж/К.
Однако, теплоёмкость – величина неопределённая, поэтому пользуются понятиями удельной и молярной теплоёмкости.
Удельная теплоёмкость (Суд) есть количество теплоты, необходимое для нагревания единицы массы вещества на 1 градус [Cуд] = Дж/К.
Для газов удобно пользоваться молярной теплоемкостью Cμ- количество теплоты, необходимое для нагревания 1 моля газа на 1 градус:
|
|
|
(4.2.2) |
[Cμ] = Дж/(моль×К).
Из п. 1.2 известно, что молярная масса – масса одного моля:
|
|
|
|
где А – атомная масса; mед - атомная единица массы; NА - число Авогадро; моль μ – количество вещества, в котором содержится число молекул, равное числу атомов в 12 г изотопа углерода 12С.
Теплоёмкость термодинамической системы зависит от того, как изменяется состояние системы при нагревании.
Если газ нагревать при постоянном объёме, то всё подводимое тепло идёт на нагревание газа, то есть изменение его внутренней энергии. Теплоёмкость при этом обозначается СV.
СР – теплоемкость при постоянном давлении. Если нагревать газ при постоянном давлении Р в сосуде с поршнем, то поршень поднимется на некоторую высоту h, то есть газ совершит работу (рис. 4.2).
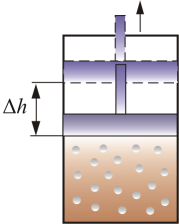 Рис.
4.2
Рис.
4.2
Следовательно, проводимое тепло
затрачивается и на нагревание и на
совершение работы. Отсюда ясно, что ![]() .
.
Итак, проводимое тепло и теплоёмкость зависят от того, каким путём осуществляется передача тепла. Значит, Q и С не являются функциями состояния.
Величины СР и СV оказываются связанными простыми соотношениями. Найдём их.
Пусть мы нагреваем один моль идеального газа при постоянном объёме(dA = 0). Тогда первое начало термодинамики запишем в виде:
|
|
|
(4.2.3) |
т.е. бесконечно малое приращение
количества теплоты ![]() равно
приращению внутренней энергии dU.
равно
приращению внутренней энергии dU.
Теплоемкость при постоянном объёме будет равна:
|
|
|
(4.2.4) |
В общем случае
|
|
|
|
так как U может зависеть не только от температуры. Но в случае идеального газа справедлива формула (4.2.4).
Из (4.2.4) следует, что ![]()
|
|
|
|
|
|
|
(4.2.5) |
Внутренняя энергия идеального газа является только функцией температуры (и не зависит от V, Р и тому подобных), поэтому формула (4.2.5) справедлива для любого процесса.
Для произвольной идеальной массы газа:
|
|
|
(4.2.6) |
При изобарическом процессе, кроме увеличения внутренней энергии, происходит совершение работы газом:
|
|
|
|
|
|
|
(4.2.7) |
Из основного уравнения молекулярно-кинетической
теории ![]() .
При изобарическом процессе Р = const.
Следовательно, из (4.2.7) получим:
.
При изобарическом процессе Р = const.
Следовательно, из (4.2.7) получим:
|
|
|
(4.2.8) |
Это уравнение Майера для одного моля газа.
Из этого следует, что физический смысл универсальной газовой постоянной в том, что R – численно равна работе, совершаемой одним молем газа при нагревании на один градус в изобарическом процессе.
Используя это соотношение, Роберт Майер в 1842 г. вычислил механический эквивалент теплоты: 1 кал = 4,19 Дж.
Полезно знать формулу Майера для удельных теплоёмкостей:
|
|
|
|
или
|
|
Адиабатический
процесс - это такое изменение состояний
газа, при котором он не отдает и не
поглощает извне теплоты. Следовательно,
адиабатический процесс характеризуется
отсутствием теплообмена газа с окружающей
средой. Адиабатическими можно считать
быстро протекающие процессы. Так как
передачи теплоты при адиабатическом
процессе не происходит, то ![]() и
уравнение I начала термодинамики
принимает вид
и
уравнение I начала термодинамики
принимает вид
|
(9.20) |
или
![]()
т.е. внешняя работа газа может производиться вследствие изменения его внутренней энергии. Адиабатное расширение газа (dV>0) сопровождается положительной внешней работой, но при этом внутренняя энергия уменьшается и газ охлаждается (dT<0).
Сжатие газа (dV0, т.е. адиабатное сжатие газа сопровождается его нагреванием.
Найдем связь между параметрами состояния идеального газа (например, Р и V) в адиабатическом процессе. Для этого перепишем (9.20) в форме
![]()
а
величину ![]() найдем
из уравнения Менделеева - Клапейрона
найдем
из уравнения Менделеева - Клапейрона
![]() Таким
образом,
Таким
образом,
![]() или,
учитывая, что для идеального
газа
или,
учитывая, что для идеального
газа ![]()
![]() Разделим
обе части этого уравнения на
Разделим
обе части этого уравнения на ![]()
![]()
где ![]() безразмерная
величина, называемая постоянной адиабаты.
Пренебрегая зависимостью
безразмерная
величина, называемая постоянной адиабаты.
Пренебрегая зависимостью ![]() от
температуры, можно считать, что для
данного газа
от
температуры, можно считать, что для
данного газа ![]() .
Интегрируя последнее уравнение
.
Интегрируя последнее уравнение
![]() получим
получим
![]() т.е.
т.е.
|
(9.21) |
Это выражение называют уравнением Пуассона. Соотношение между давлением и температурой, а также между объемом и температурой идеального газа в адиабатическом процессе имеют вид
![]()
Эти
соотношения легко получить из (9.21),
пользуясь уравнением Менделеева -
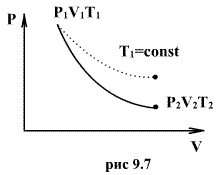
Клапейрона. Линию, изображающую
адиабатический процесс в диаграмме
состояния, называют адиабатой. На рис.
9.7 сплошной линией показан вид адиабаты
в (P-V) диаграмме. Для сравнения в том же
рисунке пунктирной линией изображена
изотерма, соответствующая температуре
газа в начальном состоянии 1. Так как
для любого идеального газа показатель
адиабаты ![]() ,
то в (P-V) диаграмме адиабата всегда идет
круче, чем изотерма. Объясняется это
тем, что при адиабатическом сжатии
увеличение давления обусловлено не
только уменьшением объема газа, как при
изотермическом сжатии, то также еще и
увеличения температуры. При адиабатическом
расширении температура газа уменьшается,
поэтому давление газа падает быстрее,
чем при изотермическом расширении.
,
то в (P-V) диаграмме адиабата всегда идет
круче, чем изотерма. Объясняется это
тем, что при адиабатическом сжатии
увеличение давления обусловлено не
только уменьшением объема газа, как при
изотермическом сжатии, то также еще и
увеличения температуры. При адиабатическом
расширении температура газа уменьшается,
поэтому давление газа падает быстрее,
чем при изотермическом расширении.
Работу, совершаемую газом в адиабатическом процессе, найдем интегрируя выражение
![]() Полная
работа
Полная
работа
![]()
Из уравнения
Майера (9.18) и выражения ![]() для
показателя адиабаты γ следует, что
для
показателя адиабаты γ следует, что
![]()
Поэтому
|
(9.22) |
В соответствии
с соотношением ![]()

Следовательно, выражение (9.22) для работы можно представить в виде
 или
или
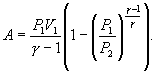
Уравнение Пуассона :
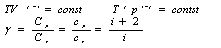
(y - показатель адиабаты или коэффициент Пуассона)
Уравнение Пуассона связывает параметры состояния газа приадиабатном процессе.
Работа в адиабатном процессе:
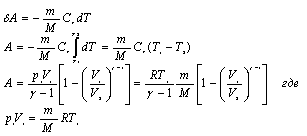

 ,
,