7. Преобразования Галилея. Кинематика относительного движения. Абсолютное, относительное и переносное ускорение частиц. Силы инерции. Центробежная сила.

Преобразования Галилея. Рассмотрим две системы отсчета движущиеся друг относительно друга и с постоянной скоростью v0.Одну из этих систем обозначим буквой K. Будем считать неподвижной. Тогда вторая система K¢ будет двигаться прямолинейно и равномерно. Выберем координатные оси x,y,z системы K и x',y',z' системы K' так что оси x и x' совпадали, а оси y и y' , z и z', были параллельны друг другу. Найдем связь между координатами x,y,z некоторой точки P в системе K и координатами x',y',z' той же точки в системе K'. Если начать отсчёт времени с того момента, когда начало координат системы, совпадали, то x=x'+v0, кроме того, очевидно, что y=y', z=z'. Добавим к этим соотношениям принятое в классической механике предположение, что время в обеих системах течёт одинаковым образом, то есть t=t'. Получим совокупность четырёх уравнений : x=x'+v0t;y=y';z=z';t=t', названных преобразованиями Галилея. Механический принцип относительности. Положение о том, что все механические явления в различных инерциальных системах отсчёта протекают одинаковым образом, вследствие чего никакими механическими опытами невозможно установить, покоится ли система или движется равномерно и прямолинейно носит названия принцип относительности Галилея. Нарушение классического закона сложения скоростей. Исходя из общего принципа относительности (никаким физическим опытом нельзя отличить одну инерциальною систему от другой), сформулированным Альбертом Эйнштейном, Лоуренс изменил преобразования Галилиея и получил : x'=(x-vt)/Ö (1-v2/c2); y'=y; z'=z; t'=(t-vx/c2)/Ö (1-v2/c2). Эти преобразования называются преобразованиями Лоуренса.

8. Механика жидкостей. Уравнение Бернулли.

Свойства жидкостей и газов во многом отличаются, однако, в ряде механических явлений их поведения являются одинаковыми параметрами и идентичными уравнениями.

Поэтому гидроаэромеханика – раздел механики, изучающий равновесие и движение жидкостей и газов, их взаимодействия между собой и обтекаемыми ими твердыми телами, - использует единый подход к изучению жидкостей и газов.

P=ΔF/ΔS - давление жидкости, [P]-1Па=1Н/м²;

Давление жидкости на дно и стенки сосуда P=ρgh называется гидростатическим. Движение жидкостей называется течением, а совокупность частиц движущейся жидкости – потоком. Графически движение жидкостей изображается с помощью линий тока, которые проводятся так, что касательные к ним совпадают по направлению с вектором скорости. Течение жидкости называется установившимся (стационарным), если форма и расположение линий тока, а также значения скоростей в каждой ее точке со временем не изменяются.

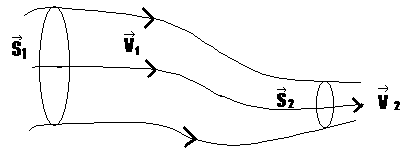
S₁V₁=S₂V₂=const (3.24) называется уравнением неразрывности для несжигаемой жидкости. Уравнение неразрывности означает, что через различные сечения трубки за одинаковый промежуток времени проходит одинаковое по объему количество жидкости. Т.е. чем меньше сечение трубки, скорость течения больше и наоборот. P=ρυ²/2 называется гидродинамическим давлением. Уравнение: ρυ²/2+ρgh₁+P₁=ρυ₂²/2+ρgh₂+P₂ (3.25) или ρυ²/2+ρgh+P=const (3.26) называется уравнением Бернулли. Для горизонтальной трубки тока выражение (3.26) примет вид: ρυ²/2+P=const (3.27), откуда следует, при течении жидкости по горизонтальной трубе, имеющей различные сечения, скорость жидкости больше в местах сужения, я статическое давление больше в более широких местах, т.е. там, где скорость меньше. Этот вывод положен в основу работы водоструйного насоса.