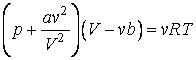21. Термодинамические потенциалы.

любая из четырех функций, определенных на множестве состояний макроскопич. (термодинамич.) системы: энергия, тепловая функция (или энтальпия), свободная энергия Гельмгольца и свободная энергия Гиббса (иногда наз. термодинамич. потенциалом в узком смысле).  При формальном построении термодинамики состояния (однокомпонентной) термодинамич. системы описываются любой из пар термодинамич. параметров (s, v),(s, р),( Т, v),( Т, р), где s- удельная энтропия системы, Т - ее абсолютная температура, р - давление и v - удельный объем. Каждой из этих пар удобно приписать свой Т. п.: паре (s, v)- энергию E=E(s, v), паре (s, р) -тепловую функцию W=W(s, р), паре ( Т, v) - свободную энергию Гельмгольца F=F(T, v )и, наконец, паре ( Т, р)- свободную энергию Гиббса Ф=Ф( Т, р).  При этом если выбрана какая-нибудь пара параметров, описывающих состояния системы, то два других параметра выражаются как частные производные соответствующего Т. п. (отсюда и название). Параметры s, Ти р, vявляются сопряженными в том смысле, что каждый из них выражается как частная производная по другому (напр., при выборе пары (s, v )с потенциалом Е(s,v)параметры Т и р):

 Переход от одной пары параметров с ее потенциалом к другой паре с соответствующим потенциалом задается с помощью Лежандра преобразования. Так, при переходе от пары (s, v) к паре ( Т, v) потенциал F( Т, v )этой пары равен

F(T,v)=-E(s(T), v) - s(T) T,

где s(T)находится из уравнения (1), т. е. F(T, v )с точностью до знака совпадает с преобразованием Лежандра функции Е(s, v )как функции переменной s. При содержательном построении термодинамики с помощью равновесных гиббсовских ансамблей Т. п. могут быть выражены с помощью термодинамич. предела, деленного на объем логарифма статистич. суммы (и его производных) какого-нибудь из гиббсовских ансамблей. Напр., свободная энергия Гельмгольца равна

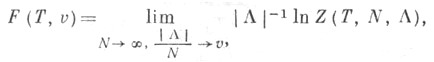
где   - статистическая сумма малого канонич. ансамбля для системы из . частиц, заключенных в области   - объем этой области   при фиксированном значении температуры Т(см. [3]).

22. Вандерваальсовский газ. Уравнение Ван-дер-Ваальса.

Как отмечалось ранее, при низких температурах и высоких давлениях уравнение Менделеева – Клапейрона для одного моля вещества

(5.2.1)

дает существенные отклонения от значений, измеряемых на опыте.

Были сделаны многочисленные попытки найти уравнение состояния для реального вещества, которое могло бы охватить, если не все состояния вещества, то хотя бы газообразное и жидкое. Из множества предложенных уравнений наибольшей известностью пользуется уравнение Ван-дер-Ваальса:

(5.2.2)

записанное для одного моля вещества. Для   молей это уравнение имеет вид:

(5.2.3)

Постоянные a и b определяются экспериментально и имеют различные значения для разного сорта молекул. Уравнение (5.1.2) не выводится, оно устанавливается введением в уже известное уравнение Менделеева – Клапейрона двух поправок. Чтобы обосновать их введение заметим, что в уравнении (5.1.2) объем означает объем сосуда, в котором содержится один моль газа. В случае идеального газа, состоящего из материальных точек, весь этот объем доступен для движения молекул. В реальном газе сами молекулы занимают некоторую часть объема сосуда, и эта часть недоступна для всех других молекул. Эту часть объема следует вычесть из объема . Тогда уравнение (5.1.2) приобретет вид

(5.2.4)

Из последнего выражения видно, что поправка b равна тому объему, который занимал бы газ при бесконечно большом давлении, т. е. молекулы реального газа не могут сблизиться друг с другом до расстояния равного нулю, даже при бесконечно большом давлении. Поэтому введение поправки b означает приблизительный учет сил отталкивания между молекулами.

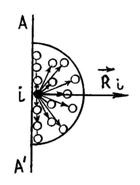
Как мы знаем, между молекулами действуют не только силы отталкивания, но и силы притяжения. Любая молекула, расположенная вблизи стенки сосуда AA' испытывает результирующую силу притяжения

(5.2.5)

со стороны молекул, расположенных в сфере действия сил притяжения.

рис. 1

Таким образом, в результате действия сил притяжения давление на стенку со стороны газа будет меньше, по сравнению с тем давлением (5.2.4), которое испытала бы стенка, если бы сил притяжения между молекулами не было, т. е.

(5.2.6)

Откуда находим уравнение Ван-дер-Ваальса:

(5.2.7)

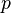•  — давление,

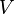•  — объём,

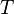•  — абсолютная температура,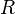

•  — универсальная газовая постоянная.

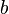•  — объем молекул газа.

Поясним появление в формуле (5.2.9) добавочного давления. Пусть газ находится в цилиндре под невесомым поршнем. Внешнее давление стремится сжать газ, т. е. сблизить его молекулы. Если бы молекулы газа друг друга не притягивали, газ испытывал бы на себе одно только внешнее давление . Но взаимное притяжение молекул, как мы выяснили, также стремится приблизить молекулы друг к другу, т. е. действует в том же направлении, как и внешнее давление . Поэтому результат притяжения молекул сказывается в кажущемся увеличении внешнего давления на газ, как будто бы к величине давления на поршень прибавилось некоторое добавочное давление .