1. Законы Ньютона

Первый закон Ньютона

Всякое тело находится в состоянии покоя или равномерного и прямолинейного движения, пока воздействие со стороны других тел не заставит его изменить это состояние.

Второй закон Ньютона

Ускорение всякого тела прямо пропорционально действующей на него силе и обратно пропорционально массе тела.

- ускорение тела;

– сила, приложенная к телу;

- масса тела;

– коэффициент пропорциональности.

В инерциальной системе отсчета производная импульса материальной точки по времени равна действующей на него силе.

- импульс тела;

;

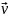– скорость тела;

- время;

– сила, приложенная к телу;

– производная по времени.

Когда на тело действуют несколько сил, с учётом принципа суперпозиции второй закон Ньютона записывается:

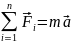
Третий закон Ньютона

Всякое действие тел друг на друга носит характер взаимодействия ; силы, с которыми действуют друг на друга взаимодействующие тела, всегда равны по величине и противоположны по направлению.

2. Законы изменения и сохранения импульса механической системы.

Закон сохранения импульса

Импульс замкнутой системы материальных точек остается постоянным.

По второму закону Ньютона:

- импульс тела;

;

– скорость тела;

- время;

– сила, приложенная к телу;

– производная по времени.

Когда на тело действуют несколько сил, с учётом принципа суперпозиции второй закон Ньютона записывается:

3. Работа силы, мощность. Консервативные и неконсервативные силы.

Работа – скалярная величина, равная произведению проекции силы на направление перемещения и пути , проходимого точной приложения силы:

; ;

Если сила и направления образуют острый угол (cos α>0), работа положительна. Если угол α – тупой (cos α<0), работа отрицательна. При работа равна нулю.

Работа, в системе СИ, измеряется в (дж).

Мощность – величина, показывающая, какую работу совершает механизм в единицу времени. Таким образом, мощность есть величина, равная отношению работы к промежутку времени , за который она совершается:

Мощность, в системе СИ, измеряется в ватт (вт), (дж/сек.).

Для сил, зависящих только от положения тел, может считаться, что работа, совершаемая ими над телом, не зависит от пути, а определяется только начальным и конечным положениями тела в пространстве. В этом случае поле сил называется потенциальным, а сами силы – консервативными. Силы, работа которых зависит от пути, по которому тело переходит из одного положения в другое, называются неконсервативными.

Работа консервативных сил на любом замкнутом пути равна нулю.

4. Универсальная связь между потенциальной энергией и силой (градиент). Закон сохранения и изменения механической энергии.

Связь между силой и потенциальной энергией.

Работа консервативных сил не зависит от формы траектории. Следовательно, потенциальная энергия, изменение которой, взятое с обратным знаком, равно этой работе, может служить характеристикой силового поля. Про тела, которые могут совершить работу, говорят, что они обладают энергией.

Потенциальная энергия - физическая величина, показывающая, какую работу могут совершить внутренние консервативные силы над телом.

Установим связь между потенциальной энергией и силами, формирующими это потенциальное поле. Рассмотрим сначала одномерное движение частицы под действием некоторой внутренней консервативной силы . Исходя из определений элементарной работы и потенциальной энергии, имеем: ;

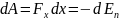Следовательно, , т.е. проекция силы есть производная от потенциальной энергии по координате. В случае трехмерного движения каждая составляющая проекции вектора силы зависит от скорости изменения потенциальной энергии в пространстве аналогичным образом. Тогда в соответствии с принципом суперпозиции вектор силы равен градиент :

Вектор называется градиентом функции f(x, y, z).

f(x, y, z) - некая произвольная функция, зависящая от переменных x, y и z;

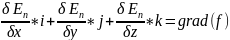
Вектор градиента направлен в сторону наиболее быстрого изменения функции. Таким образом, вектор силы равен градиенту потенциальной энергии, взятому с обратным знаком.

5. Момент силы. Момент импульса. Закон изменения и сохранения момента импульса (уравнение моментов). Уравнение динамики тела, вращающегося вокруг неподвижной оси. Момент инерции тела, простейшие примеры.

Различают два основных вида вращательного движения твердого тела:

1)   вращение вокруг неподвижной точки О, при котором все точки тела движутся по поверхностям концентрических сфер с центром в точке О; 

2)   вращение вокруг неподвижной оси Z; здесь все точки тела вращаются по окружностям, центры которых лежат на одной прямой, являющейся осью вращения Z.

Угловые характеристики: путь j, скорость w = dj/dt и ускорение e = dw/dt.

Векторные меры движения и взаимодействия, соответственно импульс Р и сила F заменяются во вращательном движении на момент импульса L и момент силы М, а мера инертности – масса m – на момент инерции J.

В качестве векторной меры вращательного движения некоторой материальной точки m_i  относительно неподвижной точки (полюса) О выбирается величина L_i, называемая моментом импульса и определяемая векторным произведением радиус-вектора r_i  материальной точки на ее импульс р_i = m_iu_i:                               L_i = [r_i, р_i]

Вектор L_i  направлен согласно правилу правого винта или из конца вектора L_i  поворот вектора r_i к вектору р_i  виден совершающимся по кратчайшему расстоянию против часовой стрелки

 Соответственно в качестве момента импульса L твердого тела (или системы материальных точек) относительно неподвижной точки О выбирается векторная величина, равная геометрической сумме моментов импульсов L_i, составляющих систему (тело) точек:  L = SL_i  = S[r_i, р_i]                                 

В качестве элементарной меры вращательного взаимодействия выбирается величина М, называемая моментом силы относительно точки и численно равная векторному произведению радиус-вектора r точки приложения силы на вектор силы F, то есть М = [r, F]. Вектор М направлен перпендикулярно плоскости векторов r и F по правилу правого винта.  Модуль вектора момента силы равен:   М = F×r×sin a  = F×l, где a - угол

между векторами r и F, а  l = r×sin a - плечо силы F, то есть длина перпендикуляра, опущенного из точки О на линию действия силы F.

Закон изменения момента импульса твердого тела (системы материальных точек) или уравнение моментов  имеет вид: dL/dt = М^внеш

– быстрота изменения момента  импульса твердого тела относительно неподвижной точки равна результирующему моменту относительно той же точки всех внешних сил, действующих на тело.

Основное уравнение М_z = Je_z динамики вращательного движения твердого тела (системы материальных точек)относительно неподвижной оси по своей структуре идентично второму закону Ньютона F = mа. Аналогом массы m в нем выступает момент инерции J твердого тела. И так же, как масса, он выступает мерой инертности тела, но применительно к вращательному движению. Чем больше момент инерции J твердого тела, тем меньшее угловое ускорение e оно приобретает под действием одного и того же момента М внешних сил, то есть тем медленнее изменяется его угловая скорость.

Основное уравнение М_z = Je_z динамики вращательного движения твердого тела (системы материальных точек)относительно неподвижной оси по своей структуре идентично второму закону Ньютона F = mа. Аналогом массы m в нем выступает момент инерции J твердого тела. И так же, как масса, он выступает мерой инертности тела, но применительно к вращательному движению. Чем больше момент инерции J твердого тела, тем меньшее угловое ускорение e оно приобретает под действием одного и того же момента М внешних сил, то есть тем медленнее изменяется его угловая скорость. Момент инерции материальной точки J_i = m_ir_i² пропорционален квадрату расстояния r_i  от точки до оси вращения. С ростом массы m и при неизменном расстоянии r до оси вращения, та же сила F сообщает материальной точке меньшее линейное ускорение (по 2-му закону Ньютона), а соответственно и угловое ускорение e = а/r. С удалением точки от оси враще­ния возрастает момент М одной и той же силы F: М = Fr  и уменьшается угловое ускорение e = а/r = F/mr, а момент инерции J = М/e = Fr/(F/mr) = mr² возрастает квадратично расстоянию до оси вращения (радиусу окружности). Момент инерции, как и масса тел, оказывается аддитивной характеристикой, то есть результирующий момент инерции твёрдого тела (системы матери­альных точек) равен сумме моментов инерции составляющих его частиц:

        J = SJ_к = Sm_кr_к²

В случае непрерывного распределения точек /массы/ сумма в выражении для момента инерции заменяется интегралом:  J = òr_к²dm  = òrr²dV

 Момент инерции тела зависит не только от его массы, но и от её распре­деления относительно оси вращения. Для некоторых симметричных и однород­ных тел момент инерции J_с относительно оси, проходящей через центр симметрии С (центр масс или центр инерции) выражается следующими формулами:

1. Колесо /обод/, полый цилиндр:  J_с = mR²

2. Диск, сплошной цилиндр: J_с = mR²/2

3. Шар: J_с = 2mR²/5

4. Стержень: J_с = ml²/12

При параллельном переносе оси вращения на расстояние а от центра инерции момент инерции тела массой m возрастает на mа², т. е. J = J_С + mа². В этом состоит суть теоремы Штейнера. Выведем эту теорему.

Дано твердое тело (система материальных точек).

Проведем две параллельные оси; одну через центр масс С тела и другую через точку О, отстоящую от центра масс на расстояние а. На рисунке оси перпендикулярны плоскости чертежа. Выделим в твердом теле некоторую элементарную массу Dm_i. Проведем в нее из точек С и О векторы R_i и r_i.                                       

Из чертежа видно, что r_i = а + R_i. Возведем это равенство в квадрат: r_i²  = а² + 2а×r_i + R_i². Умножим его на Dm_i и просуммируем по всем элементарным массам (точкам) тела: SDm_i×r_i² = а²SDm_i + 2аSDm_i×R_i  + SDm_i×R_i².

Первая сумма SDm_i×r_i²  в полученном равенстве представляет собой момент инерции J  тела относительно точки О, а последняя сумма SDm_i×R_i² представляет собой момент инерции J_С  тела относительно центра масс. Так как SDm_i равна массе m всего тела, то слагаемое  а²SDm_i = mа². И, наконец, вспоминая определение радиус-вектора центра масс:

R_С = (1/m)SDm_i×R_i, видим, что сумма SDm_i×R_i = m×R_С представляет собой произведение массы тела на радиус-векторR_С центра масс тела. Но так как здесь радиус-вектор R_С задается относительно самого центра масс, то он получается равным нулю. В итоге написанное выше равенство примет вид   J = mа² + J_С, который и представляет собой теорему Штейнера.