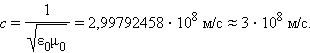33. Мощность в цепи переменного тока. Коэффициент мощности.

Электрическая мощность р в цепи с активным сопротивлением в любой момент времени равна произведению мгновенных значений силы тока i и напряжения и. Следовательно, мгновенная мощность р не является постоянной величиной, как при постоянном токе, а изменяется по кривой (см. рис. 175,б). Эту кривую можно также получить графически, перемножая ординаты кривых силы тока i и напряжения и при различных углах ?t. Изменение мощности происходит с двойной частотой ?t по отношению к изменению тока и напряжения, т. е. один период изменения мощности соответствует половине периода изменения тока и напряжения. Все значения мощности являются положительными. Физически положительное значение мощности означает, что энергия передается от источника электрической энергии к приемнику. Максимальное значение мощности при ?t = 90° и ?t = 270°

P_max = U_тI_т = 2UI

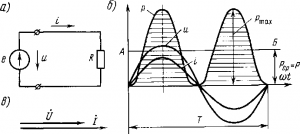Рис. 175. Схема включения в цепь переменного тока активного сопротивления (а), кривые тока i, напряжения и, мощности р (б) и векторная диаграмма (в)

Практически об энергии W, создаваемой электрическим током, судят не по максимальной мощности, а по средней мощности Р_ср = Р, так как эта энергия может быть выражена как произведение среднего значения мощности Р на время протекания тока:

W = Pt.

Кривая мгновенной мощности симметрична относительно линии АБ, которая соответствует среднему значению мощности Р. Поэтому

P = P_max / 2 = UI

Используя формулу (67) закона Ома, активную мощность можно выразить также в виде P = I²R или P=U²/R.

В электротехнике среднюю мощность, потребляемую активным сопротивлением, обычно называют активной мощностью, или просто мощностью, и обозначают буквой Р.

Коэффицие́нт мо́щности — безразмерная физическая величина, характеризующая потребителя переменного электрического тока с точки зрения наличия в нагрузке реактивной составляющей. Коэффициент мощности показывает, насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения.

Численно коэффициент мощности равен косинусу этого фазового сдвига.

Коэффициент мощности необходимо учитывать при проектировании электросетей. Низкий коэффициент мощности ведёт к увеличению доли потерь электроэнергии в электрической сети в общих потерях. Чтобы увеличить коэффициент мощности, используют компенсирующие устройства. Неверно рассчитанный коэффициент мощности может привести к избыточному потреблению электроэнергии и снижению КПД электрооборудования, питающегося от данной сети.

Для расчётов в случае гармонических переменных U (напряжение) и I (сила тока) используются следующиематематические формулы:

Здесь   — активная мощность,   — полная мощность,   — реактивная мощность.

34. Электромагнитные волны. Волновое уравнение. Уравнение плоской электромагнитной волны. Скорость электромагнитных волн.

Электромагнитная волна - процесс распространения электромагнитного поля в пространстве.

Электромагнитная волна представляет собой процесс последовательного, взаимосвязанного изменения векторов напряжённости электрического и магнитного полей, направленных перпендикулярно лучу распространения волны, при котором изменение электрического поля вызывает изменения магнитного поля, которые, в свою очередь, вызывают изменения электрического поля.

Волна (волновой процесс) - процесс распространения колебаний в сплошной среде. При распростаранении волны частицы среды не движутся вместе с волной, а колеблются около своих положений равновесия. Вместе с волной от частицы к частице среды передаются лишь состояния колебательного движения и его энергия. Поэтому основным свойством всех волн, независимо от их природы, является перенос энергии без переноса вещества

Электрические и магнитные поля могут существовать не только в веществе, но и в вакууме. Поэтому должно быть возможным распространение электромагнитных волн в вакууме.           Условием возникновения электромагнитных волн является ускоренное движение электрических зарядов. Так, изменение магнитного поля происходит                      при изменении тока в проводнике, а изменение тока происходит при изменении скорости зарядов, т. е. при движении их с ускорением. Скорость распространения электромагнитных волн в вакууме, по расчетам Максвелла, должна быть приблизительно равна 300 000 км/с.

Уравнение любой волны есть решение некоторого дифференциального уравнения, называемого волновым. Найдем общий вид волнового уравнения. Для этого продифференцируем дважды уравнение плоской волны по времени t и всем координатам:

  ,

, 

,

(5.6.1)

(5.6.2)

      Сложим уравнения (5.6.2):

.

(5.6.3)

      Подставим из (5.6.1) значение   , и получим:     . Учтем, что    ,  а окончательно получим для волнового уравнения

.

(5.6.4)

      Всякая функция, удовлетворяющая уравнению (5.6.4), описывает некоторую волну, причем корень квадратный из величины, обратной коэффициенту при производной по времени   ,  есть фазовая скорость волны.

      Используя оператор Лапласа   , волновое уравнение можно записать в виде

.

Уравнение плоской электромагнитной волны

При прохождении монохроматической электромагнитной волны частотой ω векторы E и H в данной фиксированной точке пространства испытывают синфазные и только синфазные гармонические колебания с этой же частотой Из условия синфазности следует, что в тех точках пространства, где E = 0 должно быть и H = 0, аналогично и по амплитудным значениям E₀ и H₀. 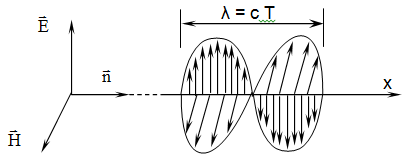Это значит, что векторная волна электрического поля E пространственно совпадает с векторной волной магнитного поля H, но только при этом векторы E и H колеблются во взаимно – перпендикулярных плоскостях, как это показано на рисунке ниже Если источником задается одно единственное направление x для излучения электромагнитной волны, то фронт волны будет плоским, а волна одномерной, как для вектораE, так и для вектора H. В этом случае волну можно представить двумя уравнениями, соответственно

Электромагнитные волны распространяются в веществе с конечной скоростью

Здесь ε и μ – диэлектрическая и магнитная проницаемости вещества, ε₀ и μ₀ – электрическая и магнитная постоянные: ε₀ = 8,85419·10^–12 Ф/м,μ₀ = 1,25664·10^–6 Гн/м.

Длина волны λ в синусоидальной волне свявзана со скоростью υ распространения волны соотношением λ = υT = υ / f, где f – частота колебаний электромагнитного поля, T = 1 / f.

Скорость электромагнитных волн в вакууме (ε = μ = 1): 

Скорость c распространения электромагнитных волн в вакууме является одной из фундаментальных физических постоянных.