28. Электромагнитные колебания. Колебательный контур. Дифференциальное уравнение. Уравнение q, I, Uc, Ul.

Периодические изменения во времени электрического заряда (силы тока, напряжения) называются электромагнитными колебаниями.

Электрическая цепь, состоящая из последовательно соединенных конденсатора с емкостью C  и катушки с индуктивностью L, наз. колебательным контуром.

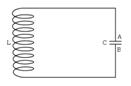
Если активное сопротивление R -> 0, то колебания являются свободными незатухающими. Возбудить колебания в контуре можно либо сообщив заряд конденсатору (электрическое поле), либо с помощью электромагнитной индукции возбудив ток в катушке (магнитное поле).

Закономерности электромагнитных и механических колебаний математически одинаковы.

Общий вид уравнения колебательного движения:  .

Уравнение гармонического колебания заряда (изменение величины электрического заряда!):  .

Колебания тока:  , т.о.   .

Напряжение на конденсаторе:

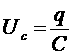
Напряжение, возникающее в катушке при изменении протекающего тока равно

29. Затухающие электромагнитные колебания. Дифференциальное уравнение. Уравнение для заряда q, коэффициент затухания, логарифмический декремент затухания. Добротность колебательной системы.

 

ЗАТУХАЮЩИЕ КОЛЕБАНИЯ - колебания с постоянно убывающей со временем амплитудой.

        Свободные колебания реальных систем всегда затухают. Затухание обусловлено в основном трением (механические системы) и сопротивлением ( в электромагнитных колебательных контурах).

Дифференциальное уравнение свободных затухающих колебаний линейной системы задается в виде

 

где s – колеблющаяся величина, описывающая тот или иной физический процесс, =const — коэффициент затухания, 0 — циклическая частота свободных незатухающих колебаний той же колебательной системы, т. е. при =0 (при отсутствии потерь энергии) называется собственной частотой колебательной системы.

Уравнение гармонического колебания заряда (изменение величины электрического заряда!):  .

    Найдем отношение значений амплитуды затухающих колебаний в моменты времени t и   (рис. 3.1):

  ,

      где β – коэффициент затухания.

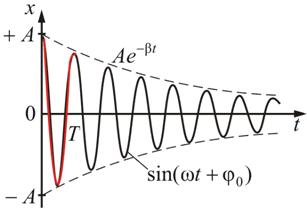
Рис. 3.1

      Натуральный логарифм отношения амплитуд, следующих друг за другом через период Т, называется логарифмическим декрементом затухания  χ:

 ;

 .

Добротность колебательной системы, отношение энергии, запасённой в колебательной системе, к энергии, теряемой системой за один период колебания. Добротность характеризует качество колебательной системы, т.к. чем больше Д. к. с., тем меньше потери энергии в системе за одно колебание. Д. к. с. Q связана с логарифмическим декрементом затухания d; при малых декрементах затухания Q " p/d. В колебательном контуре с индуктивностью L, ёмкостью C и омическим сопротивлением R Д. к. с.

30 (?). Вынужденные электромагнитные колебания. Дифференциальное уравнение. Уравнение q, I, Uc, Ul. Фазовые соотношения между колебаниями. Векторная диаграмма.

Вынужденными колебаниями называют такие колебания, которые вызываются

действием на систему внешних сил, периодически изменяющихся с течением

времени. В случае электромагнитных колебаний такой внешней силой является

периодически изменяющаяся э.д.с. источника тока.

Вынужденными электромагнитными колебаниями наз. незатухающие колебания заряда, напряжения, силы тока, вызванные периодически изменяющейся синусоидальной эдс. 

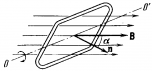
Синусоидальная эдс возникает при вращении рамки с угловой скоростью ω в стационарном магнитном поле с индукцией B. Согласно закону электромагнитной индукции

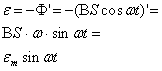
Мгновенное значение напряжения меняется по гармоническому закону  .

Мгновенное значение силы, тока пропорционально мгновенному значению напряжения и совпадает по фазе: