17.Угол между плоскостями. Условия параллельности и перпендикулярности плоскостей.

Угол между двумя пересекающимися плоскостями равен углу между прямыми, по которым они пересекаются с любой плоскостью, перпендикулярной их линии пересечения. Доказывается, что этот угол не зависит от выбора такой плоскости. Угол между двумя параллельными плоскостями принимается равным нулю.

Две плоскости α1 и α2 параллельны тогда и только тогда, когда их нормальные векторы n1 иn2 параллельны, а значит

Итак, две плоскости параллельны друг другу тогда и только тогда, когда коэффициенты при соответствующих координатах пропорциональны:

Ясно, что две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а следовательно, или

18.Различные виды уравнений прямой в пространстве ( каноническое, параметрическое, общее уравнение прямой).

Каноническое. Каноническое уравнение получается из параметрических уравнений делением одного уравнения на другое:

где — координаты и направляющего вектора прямой, и координаты точки, принадлежащей прямой.

Параметрическое. Т.к. этому уравнению удовлетворяют координаты любой точки прямой, то полученное уравнение – параметрическое уравнение прямой.

Это векторное уравнение может быть представлено в координатной форме:

Общее уравнение прямой. Линия в трехмерном пространстве определяется, вообще говоря, пересечением двух поверхностей, т.е. описывается системой двух уравнений.

Прямую в пространстве можно рассматривать как линию пересечения двух плоскостей и, следовательно, описывать системой двух линейных уравнений

A1x + B1y + C1z + D1 = 0

A2x + B2y + C2z + D2 = 0

при условии, что эти плоскости непараллельны, т.е. их нормальные векторы →n1 = {A1, B1, C1} и →n2 = {A2, B2, C2} неколлинеарны. Эта система уравнений называется общими уравнениями прямой в пространстве.

19.Условия параллельности и перпендикулярности прямых в пространстве.

Чтобы две прямые были параллельны необходимо и достаточно, чтобы направляющие векторы этих прямых были коллинеарны, т.е. их соответствующие координаты были пропорциональны.

 

 

 Чтобы две прямые были перпендикулярны необходимо и достаточно, чтобы направляющие векторы этих прямых были перпендикулярны, т.е. косинус угла между ними равен нулю.

 

20. Условия параллельности и перпендикулярности плоскости и прямой в пространстве.

Если прямая L параллельна плоскости Q, то векторы n и S перпендикулярны, а потому S*n=0,

Am+Bn+Cp=0, является условием параллельности прямой и плоскости.

Если прямая L перпендикулярна плоскости Q, то векторы n и S параллельны. Поэтому равенства

A\m=B\n=C\p, являются условием перпендикулярности прямой и плоскости.

21.Угол между прямой и плоскостью.

Синус угла   между прямой  и плоскостью  равен косинусу угла  между нормалью ( ) к плоскости и направляющим вектором прямой ( ), поскольку эти два угла в сумме равны 90°.

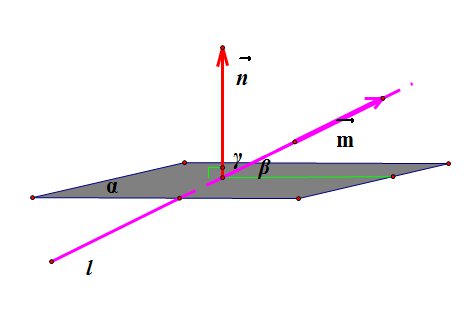
То есть синус угла  между прямой, направляющий вектор которой имеет координаты  и плоскостью, заданной уравнением  вычисляется по формуле:

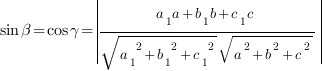
22.Окружность и ее уравнение.

Простейшей кривой второго порядка является окружность. Окружностью, радиуса Rс центром в точке M0, называется множество всех точек М плоскости , удовлетворяющих условию ММ0=R

Окружность — геометрическое место всех точек плоскости, равноудалённых от заданной точки, называемой центром, на заданное неотрицательное расстояние, называемое её радиусом

Уравнение:

Уравнению удовлетворяют координаты любой точки M(x,y)данной окружности и не удовлетворяют координаты никакой точки, не лежащей на окружности. Это каноническое уравнение окружности.

Если предположить что х0=0 и у0=0 , то получим уравнение окружности с центром в начале координат х²+у²=R².