4.Деление отрезка в заданном отношении.
1) Если
точка М(x; y) лежит на прямой, проходящей
через две данные точки
(
,
)
и
(
,
),
и дано отношение
,
в котором точка М делит отрезок
,
то координаты точки М определяются по
формулам
,
.
2)Если
точка М является серединой отрезка
,
то ее координаты определяются по
формулам
,
.
5. Понятие радиус-вектора. Разложение произвольного вектора по ортам координатных осей на плоскости и в пространстве.
Радиус-вектор-вектор, задающий положения точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.
Р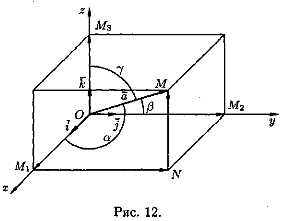
азложение
вектора по ортам координатных осей.
Рассмотрим в пространстве прямоугольную
систему координат Оxyz.
Выделим на координатных осях Ox,
Oy,Oz
единичные векторы(орты), обозначаются
i
, j,
k.
Выберем произвольный вектор а и совместим его с началом координат: а= ОМ.
Найдем проекции вектора а на координатные оси. Проведем через конец вектора ОМ плоскости, параллельные координатным плоскостям. Точки пересечения этих плоскостей с осями обозначим соответственно через М1 , М2 и Мз. Получим прямоугольный параллелепипед, одной из диагоналей которого является вектор ОМ. Тогда прха=|OM 1|, пpya = |ОМ2|, прzа=|ОМз|. По определению суммы нескольких векторов находим а = ОМ 1 + M1N + NM.
А так как M 1N=OM 2 , NM =ОМз, то
а=ОМ 1 + ОМ 2+ ОМ3 (5.1)
Обозначим проекции вектора а=ОМ на оси Ох, Оу и Oz соответственно через ах, ау и az, т.е. |OM1| = ах,|ОМ2| = ау, |ОМ3| = аz. Тогда из равенств (5.1) и (5.2) получаем
a=axi+ayj+azk (5.3)
Эта формула является основной в векторном исчислении и называется разложением вектора по ортам координатных осей. Числа ах, ау, az называются координатами вектора а, т. е. координаты вектора есть его проекции на соответствующие координатные оси.
Векторное равенство (5.3) часто записывают в символическом виде: a = (ax ;ay ;az).
Равенство b = (bx ;by ; bz ) означает, что b = bх•i+b у •j + bz • k
6.Действия с геометрическими векторами в координатной форме. Признак коллинеарности векторов.
1) при сложении векторов их координаты складываются, т.е если а=а1+а2, то Х=х1+х2, У=у1+у2, z=z1+z2
2) аналогичное правило для вычитания векторов
3) При умножении вектора на число все координаты умножаются на то же число
4) такое же правило и для деления вектора на число.
А так же:
Каждый вектор равен сумме его геометрических проекций по трем осям координат.
Каждый вектор м равен сумме произведений трех основных векторов на соответсвующие координаты вектора м
Признак Коллинеарности векторов. Коллинеарные векторы. Если векторы а1, а2 коллинеарные, то их соответствующие координаты пропорциональны: Х2:Х1=У2:У1=Z2:Z1. Если коэффициент пропорциональности положителен, то векторы а1 и а2- равнонаправленные. Если отрицателен- противоположено направлены. Абсолютное значение лямбда выражает отношение длин |а2|:|а1|
7.Скалярное произведение геометрических векторов и его свойства. Признак ортогональности векторов.
Скалярным произведением двух ненулевых векторов а и bназывается число , равное произведению длин этих векторов на косинус угла между ними.
а *b= |a|*|b|*cosa. формуле можно придать иной вид, так как|а|*cosa= проекция а на b, а |b|*cosa= проекция b на а. получаем:
а*b=|а|* проекция b на а= |b|* проекция а на b, т.е скалярное произведение двух векторов равно модулю одного из них , умноженному на проекцию другого на ось, со направленную с первым вектором .
Свойства скалярного произведения:
Переместительное свойство а*b=b*a
Сочетательное свойство (лямбда*а)*b= лямбда(а*b)
Распределительное совйство а(b+c)=ab+ac
Скалярный квадрат вектора равен квадрату его длинны а²= |а|²
i²=j²=k²=1
Если векторы а и b(ненулевые) взаимно перпендикулярны, то их скалярное произведение равно 0. Справедливо и обратное утверждение что если произведение векторов а*b=0 и а не равен 0 и b не равен 0, то они перпендикулярны. Так же i*j=j*k=k*i=0
Признак ортогональности векторов.
Два вектора называются ортогональными, если угол между ними равен прямому углу, т.е. .90 градусов